ASYMPTOTIC BEHAVIOUR FOR PRODUCTS OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS

Let 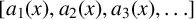$[a_1(x),a_2(x),a_3(x),\ldots ]$ be the continued fraction expansion of an irrational number 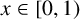$x\in [0,1)$. We are concerned with the asymptotic behaviour of the product of consecutive partial quotients of x. We prove that, for Lebesgue almost all 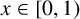$x\in [0,1)$, 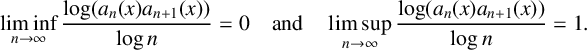$$ \begin{align*} \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} = 0\quad \text{and}\quad \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=1. \end{align*} $$

We also study the Baire category and the Hausdorff dimension of the set of points for which the above liminf and limsup have other different values and similarly analyse the weighted product of consecutive partial quotients.