截断阿贝尔数列的新同余式
IF 0.5
4区 数学
Q3 MATHEMATICS
引用次数: 0
摘要
Liu ['Supercongruences for truncated Appell series', Colloq.Math.158(2) (2019), 255-263] and Lin and Liu ['Congruences for the truncated Appell series $F_3$ and $F_4$', Integral Transforms Spec.Funct.31(1) (2020), 10-17] 确认了截断阿贝尔数列的四个超级共轭。受他们工作的启发,我们给出了截断阿贝尔数列 $F_{1}$ 的新超共假,并通过建立其 q-analogues ,给出了该超共假的两个广义。本文章由计算机程序翻译,如有差异,请以英文原文为准。
NEW CONGRUENCES FOR THE TRUNCATED APPELL SERIES
Liu [‘Supercongruences for truncated Appell series’, Colloq. Math. 158(2) (2019), 255–263] and Lin and Liu [‘Congruences for the truncated Appell series 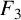 $F_3$ and
$F_3$ and 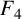 $F_4$’, Integral Transforms Spec. Funct. 31(1) (2020), 10–17] confirmed four supercongruences for truncated Appell series. Motivated by their work, we give a new supercongruence for the truncated Appell series
$F_4$’, Integral Transforms Spec. Funct. 31(1) (2020), 10–17] confirmed four supercongruences for truncated Appell series. Motivated by their work, we give a new supercongruence for the truncated Appell series 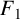 $F_{1}$, together with two generalisations of this supercongruence, by establishing its q-analogues.
$F_{1}$, together with two generalisations of this supercongruence, by establishing its q-analogues.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.20
自引率
14.30%
发文量
149
审稿时长
4-8 weeks
期刊介绍:
Bulletin of the Australian Mathematical Society aims at quick publication of original research in all branches of mathematics. Papers are accepted only after peer review but editorial decisions on acceptance or otherwise are taken quickly, normally within a month of receipt of the paper. The Bulletin concentrates on presenting new and interesting results in a clear and attractive way.
Published Bi-monthly
Published for the Australian Mathematical Society

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


