通过反射的局部自由卡尔德罗-夏波顿函数
IF 1
3区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
我们研究了与 Geiß-Leclerc-Schröer's quivers 表征相关的局部自由 Caldero-Chapoton 函数的反射,这些表征具有可对称 Cartan 矩阵的关系。我们证明,对于秩2簇代数,非初始簇变量可以表达为局部自由不可分解刚性表示的局部自由卡尔德罗-夏波顿函数。我们的方法为盖斯-勒克莱尔-施罗尔(Geiß-Leclerc-Schröer)在Dynkin情况下得到的局部自由卡尔德罗-夏波顿公式提供了新的证明。对于一般的非循环偏斜对称簇代数,我们证明了通过几乎汇和源突变得到的任何非初始簇变量的公式。本文章由计算机程序翻译,如有差异,请以英文原文为准。
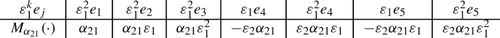
Locally free Caldero–Chapoton functions via reflections
We study the reflections of locally free Caldero–Chapoton functions associated to representations of Geiß–Leclerc–Schröer’s quivers with relations for symmetrizable Cartan matrices. We prove that for rank 2 cluster algebras, non-initial cluster variables are expressed as locally free Caldero–Chapoton functions of locally free indecomposable rigid representations. Our method gives rise to a new proof of the locally free Caldero–Chapoton formulas obtained by Geiß–Leclerc–Schröer in Dynkin cases. For general acyclic skew-symmetrizable cluster algebras, we prove the formula for any non-initial cluster variable obtained by almost sink and source mutations.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.60
自引率
0.00%
发文量
236
审稿时长
3-6 weeks
期刊介绍:
"Mathematische Zeitschrift" is devoted to pure and applied mathematics. Reviews, problems etc. will not be published.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


