具有最多诱导 4 周期或 5 周期的平面图形

IF 0.6 4区数学 Q3 MATHEMATICS

Graphs and Combinatorics Pub Date : 2024-04-05 DOI:10.1007/s00373-024-02773-w

Michael Savery

{"title":"具有最多诱导 4 周期或 5 周期的平面图形","authors":"Michael Savery","doi":"10.1007/s00373-024-02773-w","DOIUrl":null,"url":null,"abstract":"For large n we determine exactly the maximum numbers of induced \\(C_4\\) and \\(C_5\\) subgraphs that a planar graph on n vertices can contain. We show that \\(K_{2,n-2}\\) uniquely achieves this maximum in the \\(C_4\\) case, and we identify the graphs which achieve the maximum in the \\(C_5\\) case. This extends work in a paper by Hakimi and Schmeichel and a paper by Ghosh, Győri, Janzer, Paulos, Salia, and Zamora which together determine both maxima asymptotically.","PeriodicalId":12811,"journal":{"name":"Graphs and Combinatorics","volume":"92 1","pages":""},"PeriodicalIF":0.6000,"publicationDate":"2024-04-05","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Planar Graphs with the Maximum Number of Induced 4-Cycles or 5-Cycles\",\"authors\":\"Michael Savery\",\"doi\":\"10.1007/s00373-024-02773-w\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"For large n we determine exactly the maximum numbers of induced \\\\(C_4\\\\) and \\\\(C_5\\\\) subgraphs that a planar graph on n vertices can contain. We show that \\\\(K_{2,n-2}\\\\) uniquely achieves this maximum in the \\\\(C_4\\\\) case, and we identify the graphs which achieve the maximum in the \\\\(C_5\\\\) case. This extends work in a paper by Hakimi and Schmeichel and a paper by Ghosh, Győri, Janzer, Paulos, Salia, and Zamora which together determine both maxima asymptotically.\",\"PeriodicalId\":12811,\"journal\":{\"name\":\"Graphs and Combinatorics\",\"volume\":\"92 1\",\"pages\":\"\"},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2024-04-05\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Graphs and Combinatorics\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00373-024-02773-w\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Graphs and Combinatorics","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00373-024-02773-w","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

对于大 n，我们精确地确定了 n 个顶点上的平面图所包含的诱导子图（\(C_4\)和\(C_5\)）的最大数量。我们证明了在\(C_4\)情况下\(K_{2,n-2}\)唯一地达到了这个最大值，并且我们确定了在\(C_5\)情况下达到最大值的图。这扩展了哈基米和施梅切尔的论文以及戈什、居里、扬泽、保洛斯、萨利亚和萨莫拉的论文中的研究，这两篇论文共同渐近地确定了这两个最大值。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

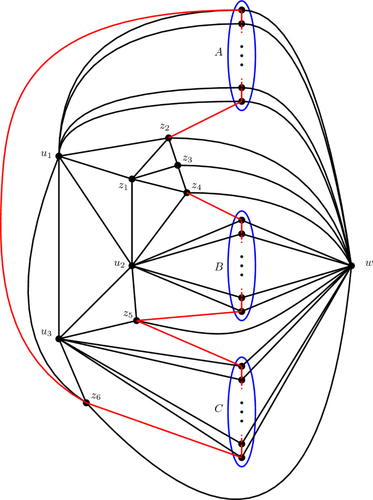
Planar Graphs with the Maximum Number of Induced 4-Cycles or 5-Cycles

查看原文本刊更多论文

Planar Graphs with the Maximum Number of Induced 4-Cycles or 5-Cycles

For large n we determine exactly the maximum numbers of induced \(C_4\) and \(C_5\) subgraphs that a planar graph on n vertices can contain. We show that \(K_{2,n-2}\) uniquely achieves this maximum in the \(C_4\) case, and we identify the graphs which achieve the maximum in the \(C_5\) case. This extends work in a paper by Hakimi and Schmeichel and a paper by Ghosh, Győri, Janzer, Paulos, Salia, and Zamora which together determine both maxima asymptotically.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Graphs and Combinatorics 数学-数学

CiteScore

1.00

自引率

14.30%

发文量

160

审稿时长

6 months

期刊介绍： Graphs and Combinatorics is an international journal devoted to research concerning all aspects of combinatorial mathematics. In addition to original research papers, the journal also features survey articles from authors invited by the editorial board.