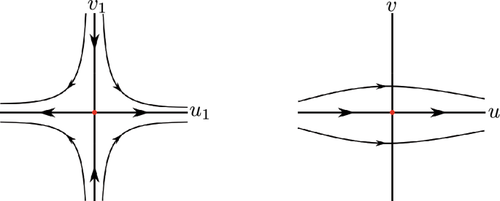
Global centers of a family of cubic systems

Consider the family of polynomial differential systems of degree 3, or simply cubic systems

$$ x' = y, \quad y' = -x + a_1 x^2 + a_2 xy + a_3 y^2 + a_4 x^3 + a_5 x^2 y + a_6 xy^2 + a_7 y^3, $$

in the plane \(\mathbb {R}^2\). An equilibrium point \((x_0,y_0)\) of a planar differential system is a center if there is a neighborhood \(\mathcal {U}\) of \((x_0,y_0)\) such that \(\mathcal {U} \backslash \{(x_0,y_0)\}\) is filled with periodic orbits. When \(\mathbb {R}^2\setminus \{(x_0,y_0)\}\) is filled with periodic orbits, then the center is a global center. For this family of cubic systems Lloyd and Pearson characterized in Lloyd and Pearson (Comput Math Appl 60:2797–2805, 2010) when the origin of coordinates is a center. We classify which of these centers are global centers.