论小维度中的巴拿赫-马祖尔距离

IF 0.6 3区数学 Q4 COMPUTER SCIENCE, THEORY & METHODS

Discrete & Computational Geometry Pub Date : 2024-04-13 DOI:10.1007/s00454-024-00641-1

Tomasz Kobos, Marin Varivoda

{"title":"论小维度中的巴拿赫-马祖尔距离","authors":"Tomasz Kobos, Marin Varivoda","doi":"10.1007/s00454-024-00641-1","DOIUrl":null,"url":null,"abstract":"We establish some results on the Banach–Mazur distance in small dimensions. Specifically, we determine the Banach–Mazur distance between the cube and its dual (the cross-polytope) in \\(\\mathbb {R}^3\\) and \\(\\mathbb {R}^4\\). In dimension three this distance is equal to \\(\\frac{9}{5}\\), and in dimension four, it is equal to 2. These findings confirm well-known conjectures, which were based on numerical data. Additionally, in dimension two, we use the asymmetry constant to provide a geometric construction of a family of convex bodies that are equidistant to all symmetric convex bodies.","PeriodicalId":50574,"journal":{"name":"Discrete & Computational Geometry","volume":null,"pages":null},"PeriodicalIF":0.6000,"publicationDate":"2024-04-13","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"On the Banach–Mazur Distance in Small Dimensions\",\"authors\":\"Tomasz Kobos, Marin Varivoda\",\"doi\":\"10.1007/s00454-024-00641-1\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We establish some results on the Banach–Mazur distance in small dimensions. Specifically, we determine the Banach–Mazur distance between the cube and its dual (the cross-polytope) in \\\\(\\\\mathbb {R}^3\\\\) and \\\\(\\\\mathbb {R}^4\\\\). In dimension three this distance is equal to \\\\(\\\\frac{9}{5}\\\\), and in dimension four, it is equal to 2. These findings confirm well-known conjectures, which were based on numerical data. Additionally, in dimension two, we use the asymmetry constant to provide a geometric construction of a family of convex bodies that are equidistant to all symmetric convex bodies.\",\"PeriodicalId\":50574,\"journal\":{\"name\":\"Discrete & Computational Geometry\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2024-04-13\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Discrete & Computational Geometry\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00454-024-00641-1\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"COMPUTER SCIENCE, THEORY & METHODS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Discrete & Computational Geometry","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00454-024-00641-1","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"COMPUTER SCIENCE, THEORY & METHODS","Score":null,"Total":0}

引用次数: 0

摘要

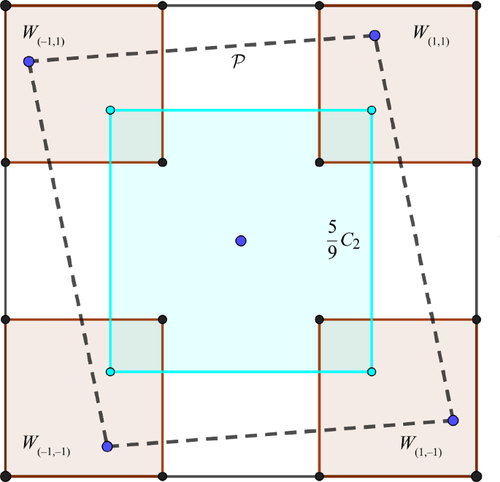
我们建立了一些关于小维度中巴拿赫-马祖尔距离的结果。具体来说，我们确定了立方体与其对偶（交叉多面体）在 \(\mathbb {R}^3\) 和 \(\mathbb {R}^4\) 中的巴纳赫-马祖尔距离。在维度三中，这个距离等于 \(\frac{9}{5}\)，而在维度四中，这个距离等于 2。这些发现证实了基于数值数据的著名猜想。此外，在二维中，我们利用不对称常数提供了与所有对称凸体等距的凸体族的几何构造。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

On the Banach–Mazur Distance in Small Dimensions

查看原文本刊更多论文

On the Banach–Mazur Distance in Small Dimensions

We establish some results on the Banach–Mazur distance in small dimensions. Specifically, we determine the Banach–Mazur distance between the cube and its dual (the cross-polytope) in \(\mathbb {R}^3\) and \(\mathbb {R}^4\). In dimension three this distance is equal to \(\frac{9}{5}\), and in dimension four, it is equal to 2. These findings confirm well-known conjectures, which were based on numerical data. Additionally, in dimension two, we use the asymmetry constant to provide a geometric construction of a family of convex bodies that are equidistant to all symmetric convex bodies.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Discrete & Computational Geometry 数学-计算机：理论方法

CiteScore

1.80

自引率

12.50%

发文量

审稿时长

6-12 weeks

期刊介绍： Discrete & Computational Geometry (DCG) is an international journal of mathematics and computer science, covering a broad range of topics in which geometry plays a fundamental role. It publishes papers on such topics as configurations and arrangements, spatial subdivision, packing, covering, and tiling, geometric complexity, polytopes, point location, geometric probability, geometric range searching, combinatorial and computational topology, probabilistic techniques in computational geometry, geometric graphs, geometry of numbers, and motion planning.