晶格复双曲三角群的镜像稳定器
IF 0.5
4区 数学
Q3 MATHEMATICS
引用次数: 0
摘要
对于每个格子复双曲三角群,我们研究复反射镜像(每个群轨道的 reprentatives)的富奇稳定器。我们给出了稳定器的明确生成器,并计算了它们在福氏群意义上的签名。对于某些群,我们还找到了明确的复线对,使得它们的稳定器的联合产生了环境晶格。本文章由计算机程序翻译,如有差异,请以英文原文为准。
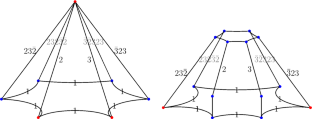
Mirror stabilizers for lattice complex hyperbolic triangle groups
For each lattice complex hyperbolic triangle group, we study the Fuchsian stabilizers of (reprentatives of each group orbit of) mirrors of complex reflections. We give explicit generators for the stabilizers, and compute their signature in the sense of Fuchsian groups. For some groups, we also find explicit pairs of complex lines such that the union of their stabilizers generate the ambient lattice.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Geometriae Dedicata
数学-数学
CiteScore
0.90
自引率
0.00%
发文量
78
审稿时长
4-8 weeks
期刊介绍:
Geometriae Dedicata concentrates on geometry and its relationship to topology, group theory and the theory of dynamical systems.
Geometriae Dedicata aims to be a vehicle for excellent publications in geometry and related areas. Features of the journal will include:
A fast turn-around time for articles.
Special issues centered on specific topics.
All submitted papers should include some explanation of the context of the main results.
Geometriae Dedicata was founded in 1972 on the initiative of Hans Freudenthal in Utrecht, the Netherlands, who viewed geometry as a method rather than as a field. The present Board of Editors tries to continue in this spirit. The steady growth of the journal since its foundation is witness to the validity of the founder''s vision and to the success of the Editors'' mission.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


