双速深床过滤方程的行波解决方案

IF 0.3 Q4 MECHANICS

Moscow University Mechanics Bulletin Pub Date : 2024-03-23 DOI:10.3103/S0027133023060018

N. E. Leontiev, K. Taurbaeva

{"title":"双速深床过滤方程的行波解决方案","authors":"N. E. Leontiev, K. Taurbaeva","doi":"10.3103/S0027133023060018","DOIUrl":null,"url":null,"abstract":"<p>Traveling wave solutions to the deep bed filtration system are constructed for a model with different velocities of a carrier fluid and suspended particles. The solution in quadratures is obtained when the velocity of the carrier fluid and that of the particles differ by a concentration-dependent factor. For some special cases, the physically realizable domains are found in the space of governing parameters. The solutions that may be interpreted as a clogging wave structure are presented.</p>","PeriodicalId":710,"journal":{"name":"Moscow University Mechanics Bulletin","volume":"78 6","pages":"159 - 164"},"PeriodicalIF":0.3000,"publicationDate":"2024-03-23","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Traveling Wave Solutions to Equations of Two-Velocity Deep Bed Filtration\",\"authors\":\"N. E. Leontiev, K. Taurbaeva\",\"doi\":\"10.3103/S0027133023060018\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>Traveling wave solutions to the deep bed filtration system are constructed for a model with different velocities of a carrier fluid and suspended particles. The solution in quadratures is obtained when the velocity of the carrier fluid and that of the particles differ by a concentration-dependent factor. For some special cases, the physically realizable domains are found in the space of governing parameters. The solutions that may be interpreted as a clogging wave structure are presented.</p>\",\"PeriodicalId\":710,\"journal\":{\"name\":\"Moscow University Mechanics Bulletin\",\"volume\":\"78 6\",\"pages\":\"159 - 164\"},\"PeriodicalIF\":0.3000,\"publicationDate\":\"2024-03-23\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Moscow University Mechanics Bulletin\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://link.springer.com/article/10.3103/S0027133023060018\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"MECHANICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Moscow University Mechanics Bulletin","FirstCategoryId":"1085","ListUrlMain":"https://link.springer.com/article/10.3103/S0027133023060018","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"MECHANICS","Score":null,"Total":0}

引用次数: 0

摘要

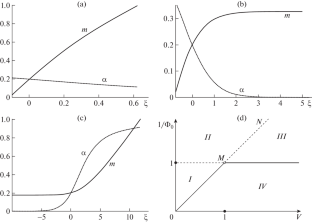
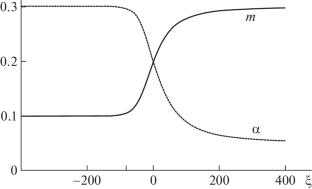
摘要针对载流体和悬浮颗粒速度不同的模型，构建了深床过滤系统的行波解。当载流体和颗粒的速度相差一个随浓度变化的因子时，可得到四元解。在某些特殊情况下，可以在控制参数空间中找到物理可实现域。该方程给出了可解释为堵塞波结构的解。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

Traveling Wave Solutions to Equations of Two-Velocity Deep Bed Filtration

查看原文本刊更多论文

Traveling Wave Solutions to Equations of Two-Velocity Deep Bed Filtration

Traveling wave solutions to the deep bed filtration system are constructed for a model with different velocities of a carrier fluid and suspended particles. The solution in quadratures is obtained when the velocity of the carrier fluid and that of the particles differ by a concentration-dependent factor. For some special cases, the physically realizable domains are found in the space of governing parameters. The solutions that may be interpreted as a clogging wave structure are presented.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Moscow University Mechanics Bulletin MECHANICS-

CiteScore

0.60

自引率

0.00%

发文量

期刊介绍： Moscow University Mechanics Bulletin is the journal of scientific publications, reflecting the most important areas of mechanics at Lomonosov Moscow State University. The journal is dedicated to research in theoretical mechanics, applied mechanics and motion control, hydrodynamics, aeromechanics, gas and wave dynamics, theory of elasticity, theory of elasticity and mechanics of composites.