气体动力学模拟中高阶逼近线性方案的实际精度
IF 0.7
4区 数学
Q3 MATHEMATICS, APPLIED
Computational Mathematics and Mathematical Physics
Pub Date : 2024-03-21
DOI:10.1134/s0965542524010044
引用次数: 0
摘要
摘要 考虑了一维气体动力学方程的新测试问题。问题的初始数据为周期性平滑波。气体流在有限时间内形成冲击波。分析了两种三阶精确线性方案(即双紧凑方案和 Rusanov 方案)在网格细化条件下的收敛性。结果表明,这两种方案在冲击影响区都只有一阶积分收敛。然而,当应用于等熵气体动力学方程时,这两种方案至少具有二阶收敛性。本文章由计算机程序翻译,如有差异,请以英文原文为准。
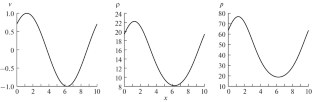
Actual Accuracy of Linear Schemes of High-Order Approximation in Gasdynamic Simulations
Abstract
A new test problem for one-dimensional gas dynamics equations is considered. Initial data in the problem is a periodic smooth wave. Shock waves are formed in the gas flow over a finite time. The convergence under mesh refinement is analyzed for two third-order accurate linear schemes, namely, a bicompact scheme and Rusanov’s scheme. It is demonstrated that both schemes have only the first order of integral convergence in the shock influence area. However, when applied to equations of isentropic gas dynamics, the schemes converge with at least the second order.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Computational Mathematics and Mathematical Physics
MATHEMATICS, APPLIED-PHYSICS, MATHEMATICAL
CiteScore
1.50
自引率
14.30%
发文量
125
审稿时长
4-8 weeks
期刊介绍:
Computational Mathematics and Mathematical Physics is a monthly journal published in collaboration with the Russian Academy of Sciences. The journal includes reviews and original papers on computational mathematics, computational methods of mathematical physics, informatics, and other mathematical sciences. The journal welcomes reviews and original articles from all countries in the English or Russian language.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


