一些分数抛物方程解的无穷衰减

IF 1.3 3区数学 Q1 MATHEMATICS

Proceedings of the Royal Society of Edinburgh Section A-Mathematics Pub Date : 2024-03-14 DOI:10.1017/prm.2024.9

Agnid Banerjee, Abhishek Ghosh

引用次数: 0

摘要

对于 $s\in [\tfrac {1}{2},\, 1)$，让 $u$ 在 $\mathbb {R}^{n} 中求解 $(\partial _t -\Delta )^s u = Vu$。\对于某个 $T>0$，$||V||_{ C^2(\mathbb {R}^{n \times [-T, 0])} < \infty$。我们证明，如果对于某个 $0<\mathfrak {K} < T$ 和 $\epsilon >；0$\[ {\unicode{x2A0D}}-_{[-\mathfrak{K},\, 0]} u^2(x, t) {\rm d}t \leq Ce^{-|x|^{2+\epsilon}}\ forall x \in \mathbb{R}^n, \]那么 $u \equiv 0$ in $\mathbb{R}^{n}.\times [-T,\, 0]$.

本文章由计算机程序翻译，如有差异，请以英文原文为准。

查看原文本刊更多论文

Decay at infinity for solutions to some fractional parabolic equations

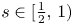For $s\in [\tfrac {1}{2},\, 1)$, let $u$ 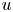solve $(\partial _t - \Delta )^s u = Vu$ 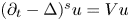in $\mathbb {R}^{n} \times [-T,\, 0]$ 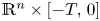for some $T>0$ 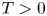where $||V||_{ C^2(\mathbb {R}^n \times [-T, 0])} < \infty$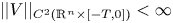. We show that if for some $0<\mathfrak {K} < T$ 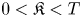and $\epsilon >0$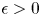\[ {\unicode{x2A0D}}-_{[-\mathfrak{K},\, 0]} u^2(x, t) {\rm d}t \leq Ce^{-|x|^{2+\epsilon}}\ \forall x \in \mathbb{R}^n, \]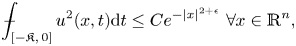then $u \equiv 0$ 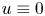in $\mathbb {R}^{n} \times [-T,\, 0]$.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Proceedings of the Royal Society of Edinburgh Section A-Mathematics 数学-数学

CiteScore

3.00

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： A flagship publication of The Royal Society of Edinburgh, Proceedings A is a prestigious, general mathematics journal publishing peer-reviewed papers of international standard across the whole spectrum of mathematics, but with the emphasis on applied analysis and differential equations. An international journal, publishing six issues per year, Proceedings A has been publishing the highest-quality mathematical research since 1884. Recent issues have included a wealth of key contributors and considered research papers.