幂等生成数
IF 0.5
4区 数学
Q3 MATHEMATICS
引用次数: 0
摘要
计算了交换环上有限正集的入射代数的最小幂生子数。这个数量要么等于 $\lceil \log _2 n\rceil $,要么等于 $\lceil \log _2 n\rceil +1 $,其中 n 是正集的万有引力。这两种情况可以通过将正集的哈塞图嵌入超立方图的补集来区分。本文章由计算机程序翻译,如有差异,请以英文原文为准。
IDEMPOTENT GENERATORS OF INCIDENCE ALGEBRAS
The minimum number of idempotent generators is calculated for an incidence algebra of a finite poset over a commutative ring. This quantity equals either 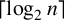 $\lceil \log _2 n\rceil $ or
$\lceil \log _2 n\rceil $ or 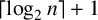 $\lceil \log _2 n\rceil +1$, where n is the cardinality of the poset. The two cases are separated in terms of the embedding of the Hasse diagram of the poset into the complement of the hypercube graph.
$\lceil \log _2 n\rceil +1$, where n is the cardinality of the poset. The two cases are separated in terms of the embedding of the Hasse diagram of the poset into the complement of the hypercube graph.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.20
自引率
14.30%
发文量
149
审稿时长
4-8 weeks
期刊介绍:
Bulletin of the Australian Mathematical Society aims at quick publication of original research in all branches of mathematics. Papers are accepted only after peer review but editorial decisions on acceptance or otherwise are taken quickly, normally within a month of receipt of the paper. The Bulletin concentrates on presenting new and interesting results in a clear and attractive way.
Published Bi-monthly
Published for the Australian Mathematical Society

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


