Invariant measures and large deviation principles for stochastic Schrödinger delay lattice systems

This paper is concerned with stochastic Schrödinger delay lattice systems with both locally Lipschitz drift and diffusion terms. Based on the uniform estimates and the equicontinuity of the segment of the solution in probability, we show the tightness of a family of probability distributions of the solution and its segment process, and hence the existence of invariant measures on $l^2\times L^2((-\rho,\,0);l^2)$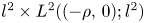 with $\rho >0$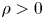. We also establish a large deviation principle for the solutions with small noise by the weak convergence method.