Qualitative properties of solutions for system involving the fractional Laplacian

In this paper, we consider the following non-linear system involving the fractional Laplacian0.1\begin{equation} \left\{\begin{array}{@{}ll} (-\Delta)^{s} u (x)= f(u,\,v), \\ (-\Delta)^{s} v (x)= g(u,\,v), \end{array} \right. \end{equation}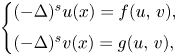in two different types of domains, one is bounded, and the other is an infinite cylinder, where $0< s<1$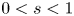. We employ the direct sliding method for fractional Laplacian, different from the conventional extension and moving planes methods, to derive the monotonicity of solutions for (0.1) in $x_n$ 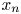variable. Meanwhile, we develop a new iteration method for systems in the proofs. Hopefully, the iteration method can also be applied to solve other problems.