求解矩阵方程 A𝒱-𝒱‾B=C 的移位分割雅各比梯度迭代算法

Optimal Control Applications and Methods Pub Date : 2024-02-21 DOI:10.1002/oca.3112

Ahmed M. E. Bayoumi

{"title":"求解矩阵方程 A𝒱-𝒱‾B=C 的移位分割雅各比梯度迭代算法","authors":"Ahmed M. E. Bayoumi","doi":"10.1002/oca.3112","DOIUrl":null,"url":null,"abstract":"To improve the convergence of the gradient iterative (GI) algorithm and the Jacobi-gradient iterative (JGI) algorithm [Bayoumi, Appl Math Inf Sci, 2021], a shift-splitting Jacobi-gradient iterative (SSJGI) algorithm for solving the matrix equation <mjx-container aria-label=\"upper A script upper V minus script upper V overbar upper B equals upper C\" ctxtmenu_counter=\"1\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\"><mjx-mrow data-semantic-children=\"13,8\" data-semantic-content=\"7\" data-semantic- data-semantic-role=\"equality\" data-semantic-speech=\"upper A script upper V minus script upper V overbar upper B equals upper C\" data-semantic-type=\"relseq\"><mjx-mrow data-semantic-children=\"10,12\" data-semantic-content=\"2\" data-semantic- data-semantic-parent=\"14\" data-semantic-role=\"subtraction\" data-semantic-type=\"infixop\"><mjx-mrow data-semantic-annotation=\"clearspeak:simple;clearspeak:unit\" data-semantic-children=\"0,1\" data-semantic-content=\"9\" data-semantic- data-semantic-parent=\"13\" data-semantic-role=\"implicit\" data-semantic-type=\"infixop\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"10\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-mo data-semantic-added=\"true\" data-semantic- data-semantic-operator=\"infixop,⁢\" data-semantic-parent=\"10\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\" style=\"margin-left: 0.056em; margin-right: 0.056em;\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"script\" data-semantic- data-semantic-parent=\"10\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi></mjx-mrow><mjx-mo data-semantic- data-semantic-operator=\"infixop,−\" data-semantic-parent=\"13\" data-semantic-role=\"subtraction\" data-semantic-type=\"operator\" rspace=\"4\" space=\"4\"><mjx-c></mjx-c></mjx-mo><mjx-mrow data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"5,6\" data-semantic-content=\"11\" data-semantic- data-semantic-parent=\"13\" data-semantic-role=\"implicit\" data-semantic-type=\"infixop\"><mjx-mover data-semantic-children=\"3,4\" data-semantic- data-semantic-parent=\"12\" data-semantic-role=\"latinletter\" data-semantic-type=\"overscore\"><mjx-over style=\"padding-bottom: 0.2em; padding-left: 0.171em; margin-bottom: -0.385em;\"><mjx-mo data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"overaccent\" data-semantic-type=\"punctuation\" size=\"s\"><mjx-stretchy-h style=\"width: 1.202em;\"><mjx-ext><mjx-c></mjx-c></mjx-ext></mjx-stretchy-h></mjx-mo></mjx-over><mjx-base><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"script\" data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi></mjx-base></mjx-mover><mjx-mo data-semantic-added=\"true\" data-semantic- data-semantic-operator=\"infixop,⁢\" data-semantic-parent=\"12\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\" style=\"margin-left: 0.056em; margin-right: 0.056em;\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"12\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-mrow><mjx-mo data-semantic- data-semantic-operator=\"relseq,=\" data-semantic-parent=\"14\" data-semantic-role=\"equality\" data-semantic-type=\"relation\" rspace=\"5\" space=\"5\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"14\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-math><mjx-assistive-mml aria-hidden=\"true\" display=\"inline\" unselectable=\"on\"><math altimg=\"/cms/asset/4de835db-dcf2-4eeb-acc4-9a5ccf422c4e/oca3112-math-0002.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><mrow data-semantic-=\"\" data-semantic-children=\"13,8\" data-semantic-content=\"7\" data-semantic-role=\"equality\" data-semantic-speech=\"upper A script upper V minus script upper V overbar upper B equals upper C\" data-semantic-type=\"relseq\"><mrow data-semantic-=\"\" data-semantic-children=\"10,12\" data-semantic-content=\"2\" data-semantic-parent=\"14\" data-semantic-role=\"subtraction\" data-semantic-type=\"infixop\"><mrow data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple;clearspeak:unit\" data-semantic-children=\"0,1\" data-semantic-content=\"9\" data-semantic-parent=\"13\" data-semantic-role=\"implicit\" data-semantic-type=\"infixop\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"10\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">A</mi><mo data-semantic-=\"\" data-semantic-added=\"true\" data-semantic-operator=\"infixop,⁢\" data-semantic-parent=\"10\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\">⁢</mo><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"script\" data-semantic-parent=\"10\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">𝒱</mi></mrow><mo data-semantic-=\"\" data-semantic-operator=\"infixop,−\" data-semantic-parent=\"13\" data-semantic-role=\"subtraction\" data-semantic-type=\"operator\">−</mo><mrow data-semantic-=\"\" data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"5,6\" data-semantic-content=\"11\" data-semantic-parent=\"13\" data-semantic-role=\"implicit\" data-semantic-type=\"infixop\"><mover accent=\"false\" data-semantic-=\"\" data-semantic-children=\"3,4\" data-semantic-parent=\"12\" data-semantic-role=\"latinletter\" data-semantic-type=\"overscore\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"script\" data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">𝒱</mi><mo data-semantic-=\"\" data-semantic-parent=\"5\" data-semantic-role=\"overaccent\" data-semantic-type=\"punctuation\">‾</mo></mover><mo data-semantic-=\"\" data-semantic-added=\"true\" data-semantic-operator=\"infixop,⁢\" data-semantic-parent=\"12\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\">⁢</mo><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"12\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">B</mi></mrow></mrow><mo data-semantic-=\"\" data-semantic-operator=\"relseq,=\" data-semantic-parent=\"14\" data-semantic-role=\"equality\" data-semantic-type=\"relation\">=</mo><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"14\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">C</mi></mrow></math></mjx-assistive-mml></mjx-container> is presented in this paper, which is based on the splitting of the coefficient matrices. The proposed algorithm converges to the exact solution for any initial value with some conditions. To demonstrate the effectiveness of the SSJGI algorithm and to compare it to the GI algorithm and the JGI algorithm [Bayoumi, Appl Math Inf Sci, 2021], numerical examples are provided.","PeriodicalId":501055,"journal":{"name":"Optimal Control Applications and Methods","volume":null,"pages":null},"PeriodicalIF":0.0000,"publicationDate":"2024-02-21","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"A shift-splitting Jacobi-gradient iterative algorithm for solving the matrix equation A𝒱−𝒱‾B=C\",\"authors\":\"Ahmed M. E. Bayoumi\",\"doi\":\"10.1002/oca.3112\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"To improve the convergence of the gradient iterative (GI) algorithm and the Jacobi-gradient iterative (JGI) algorithm [Bayoumi, Appl Math Inf Sci, 2021], a shift-splitting Jacobi-gradient iterative (SSJGI) algorithm for solving the matrix equation <mjx-container aria-label=\\\"upper A script upper V minus script upper V overbar upper B equals upper C\\\" ctxtmenu_counter=\\\"1\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\"><mjx-mrow data-semantic-children=\\\"13,8\\\" data-semantic-content=\\\"7\\\" data-semantic- data-semantic-role=\\\"equality\\\" data-semantic-speech=\\\"upper A script upper V minus script upper V overbar upper B equals upper C\\\" data-semantic-type=\\\"relseq\\\"><mjx-mrow data-semantic-children=\\\"10,12\\\" data-semantic-content=\\\"2\\\" data-semantic- data-semantic-parent=\\\"14\\\" data-semantic-role=\\\"subtraction\\\" data-semantic-type=\\\"infixop\\\"><mjx-mrow data-semantic-annotation=\\\"clearspeak:simple;clearspeak:unit\\\" data-semantic-children=\\\"0,1\\\" data-semantic-content=\\\"9\\\" data-semantic- data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"implicit\\\" data-semantic-type=\\\"infixop\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"10\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-mo data-semantic-added=\\\"true\\\" data-semantic- data-semantic-operator=\\\"infixop,⁢\\\" data-semantic-parent=\\\"10\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\" style=\\\"margin-left: 0.056em; margin-right: 0.056em;\\\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"script\\\" data-semantic- data-semantic-parent=\\\"10\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi></mjx-mrow><mjx-mo data-semantic- data-semantic-operator=\\\"infixop,−\\\" data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"subtraction\\\" data-semantic-type=\\\"operator\\\" rspace=\\\"4\\\" space=\\\"4\\\"><mjx-c></mjx-c></mjx-mo><mjx-mrow data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"5,6\\\" data-semantic-content=\\\"11\\\" data-semantic- data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"implicit\\\" data-semantic-type=\\\"infixop\\\"><mjx-mover data-semantic-children=\\\"3,4\\\" data-semantic- data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"overscore\\\"><mjx-over style=\\\"padding-bottom: 0.2em; padding-left: 0.171em; margin-bottom: -0.385em;\\\"><mjx-mo data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"overaccent\\\" data-semantic-type=\\\"punctuation\\\" size=\\\"s\\\"><mjx-stretchy-h style=\\\"width: 1.202em;\\\"><mjx-ext><mjx-c></mjx-c></mjx-ext></mjx-stretchy-h></mjx-mo></mjx-over><mjx-base><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"script\\\" data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi></mjx-base></mjx-mover><mjx-mo data-semantic-added=\\\"true\\\" data-semantic- data-semantic-operator=\\\"infixop,⁢\\\" data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\" style=\\\"margin-left: 0.056em; margin-right: 0.056em;\\\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-mrow><mjx-mo data-semantic- data-semantic-operator=\\\"relseq,=\\\" data-semantic-parent=\\\"14\\\" data-semantic-role=\\\"equality\\\" data-semantic-type=\\\"relation\\\" rspace=\\\"5\\\" space=\\\"5\\\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"14\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-math><mjx-assistive-mml aria-hidden=\\\"true\\\" display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"/cms/asset/4de835db-dcf2-4eeb-acc4-9a5ccf422c4e/oca3112-math-0002.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><mrow data-semantic-=\\\"\\\" data-semantic-children=\\\"13,8\\\" data-semantic-content=\\\"7\\\" data-semantic-role=\\\"equality\\\" data-semantic-speech=\\\"upper A script upper V minus script upper V overbar upper B equals upper C\\\" data-semantic-type=\\\"relseq\\\"><mrow data-semantic-=\\\"\\\" data-semantic-children=\\\"10,12\\\" data-semantic-content=\\\"2\\\" data-semantic-parent=\\\"14\\\" data-semantic-role=\\\"subtraction\\\" data-semantic-type=\\\"infixop\\\"><mrow data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple;clearspeak:unit\\\" data-semantic-children=\\\"0,1\\\" data-semantic-content=\\\"9\\\" data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"implicit\\\" data-semantic-type=\\\"infixop\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"10\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">A</mi><mo data-semantic-=\\\"\\\" data-semantic-added=\\\"true\\\" data-semantic-operator=\\\"infixop,⁢\\\" data-semantic-parent=\\\"10\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\">⁢</mo><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"script\\\" data-semantic-parent=\\\"10\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">𝒱</mi></mrow><mo data-semantic-=\\\"\\\" data-semantic-operator=\\\"infixop,−\\\" data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"subtraction\\\" data-semantic-type=\\\"operator\\\">−</mo><mrow data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"5,6\\\" data-semantic-content=\\\"11\\\" data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"implicit\\\" data-semantic-type=\\\"infixop\\\"><mover accent=\\\"false\\\" data-semantic-=\\\"\\\" data-semantic-children=\\\"3,4\\\" data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"overscore\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"script\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">𝒱</mi><mo data-semantic-=\\\"\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"overaccent\\\" data-semantic-type=\\\"punctuation\\\">‾</mo></mover><mo data-semantic-=\\\"\\\" data-semantic-added=\\\"true\\\" data-semantic-operator=\\\"infixop,⁢\\\" data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\">⁢</mo><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">B</mi></mrow></mrow><mo data-semantic-=\\\"\\\" data-semantic-operator=\\\"relseq,=\\\" data-semantic-parent=\\\"14\\\" data-semantic-role=\\\"equality\\\" data-semantic-type=\\\"relation\\\">=</mo><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"14\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">C</mi></mrow></math></mjx-assistive-mml></mjx-container> is presented in this paper, which is based on the splitting of the coefficient matrices. The proposed algorithm converges to the exact solution for any initial value with some conditions. To demonstrate the effectiveness of the SSJGI algorithm and to compare it to the GI algorithm and the JGI algorithm [Bayoumi, Appl Math Inf Sci, 2021], numerical examples are provided.\",\"PeriodicalId\":501055,\"journal\":{\"name\":\"Optimal Control Applications and Methods\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.0000,\"publicationDate\":\"2024-02-21\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Optimal Control Applications and Methods\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://doi.org/10.1002/oca.3112\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"\",\"JCRName\":\"\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Optimal Control Applications and Methods","FirstCategoryId":"1085","ListUrlMain":"https://doi.org/10.1002/oca.3112","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"","JCRName":"","Score":null,"Total":0}

引用次数: 0

摘要

为了提高梯度迭代（GI）算法和雅各比梯度迭代（JGI）算法[Bayoumi，Appl Math Inf Sci，2021]的收敛性，本文提出了一种基于系数矩阵拆分的求解矩阵方程 A𝒱-𝒱‾B=C的移位拆分雅各比梯度迭代（SSJGI）算法。所提出的算法在某些条件下对任何初始值都能收敛到精确解。为了证明 SSJGI 算法的有效性，并将其与 GI 算法和 JGI 算法 [Bayoumi, Appl Math Inf Sci, 2021] 进行比较，本文提供了数值示例。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

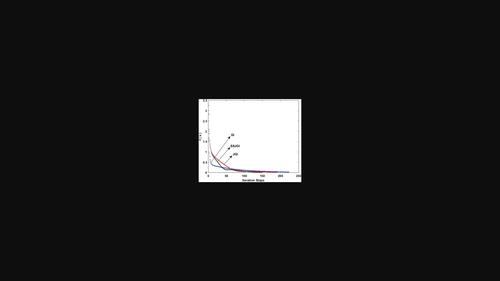
A shift-splitting Jacobi-gradient iterative algorithm for solving the matrix equation A𝒱−𝒱‾B=C

查看原文本刊更多论文

A shift-splitting Jacobi-gradient iterative algorithm for solving the matrix equation A𝒱−𝒱‾B=C

To improve the convergence of the gradient iterative (GI) algorithm and the Jacobi-gradient iterative (JGI) algorithm [Bayoumi, Appl Math Inf Sci, 2021], a shift-splitting Jacobi-gradient iterative (SSJGI) algorithm for solving the matrix equation

A 𝒱 - \overline{𝒱} B = C

is presented in this paper, which is based on the splitting of the coefficient matrices. The proposed algorithm converges to the exact solution for any initial value with some conditions. To demonstrate the effectiveness of the SSJGI algorithm and to compare it to the GI algorithm and the JGI algorithm [Bayoumi, Appl Math Inf Sci, 2021], numerical examples are provided.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Optimal Control Applications and Methods

自引率

0.00%

发文量