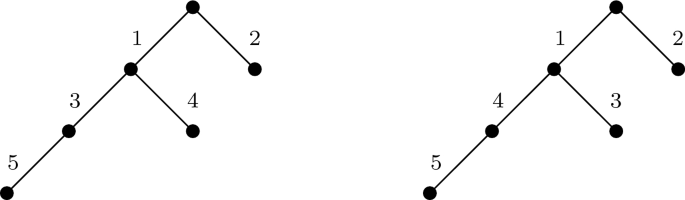
Multipermutations and Stirling Multipermutations

We consider multipermutations and a certain partial order, the weak Bruhat order, on this set. This generalizes the Bruhat order for permutations, and is defined in terms of containment of inversions. Different characterizations of this order are given. We also study special multipermutations called Stirling multipermutations and their properties.