最小化诱导阻力的普朗特 1933 模型改进版
IF 1.6
2区 数学
Q2 MATHEMATICS, APPLIED
引用次数: 0
摘要
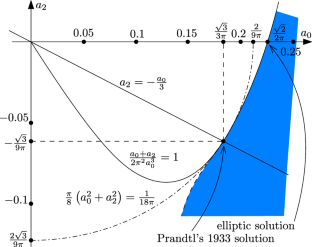
我们考虑了普朗特尔的 1933 模型,该模型用于计算有限机翼的环流分布函数 (\\Gamma \),在规定的总升力和惯性矩的约束下,该模型使诱导阻力最小。我们证明了在适当的函数空间中存在一个问题的全局最小值,而没有非负性的限制(\\Gamma \ge 0\ )。我们还考虑了一个改进的模型,其中规定的惯性矩考虑到了机翼本身重量引起的弯矩,这导致了比普朗特尔 1933 年结果更有效的解决方案。本文章由计算机程序翻译,如有差异,请以英文原文为准。
An Improvement to Prandtl’s 1933 Model for Minimizing Induced Drag
We consider Prandtl’s 1933 model for calculating circulation distribution function \(\Gamma \) of a finite wing which minimizes induced drag, under the constraints of prescribed total lift and moment of inertia. We prove existence of a global minimizer of the problem without the restriction of nonnegativity \(\Gamma \ge 0\) in an appropriate function space. We also consider an improved model, where the prescribed moment of inertia takes into account the bending moment due to the weight of the wing itself, which leads to a more efficient solution than Prandtl’s 1933 result.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
3.30
自引率
5.60%
发文量
103
审稿时长
>12 weeks
期刊介绍:
The Applied Mathematics and Optimization Journal covers a broad range of mathematical methods in particular those that bridge with optimization and have some connection with applications. Core topics include calculus of variations, partial differential equations, stochastic control, optimization of deterministic or stochastic systems in discrete or continuous time, homogenization, control theory, mean field games, dynamic games and optimal transport. Algorithmic, data analytic, machine learning and numerical methods which support the modeling and analysis of optimization problems are encouraged. Of great interest are papers which show some novel idea in either the theory or model which include some connection with potential applications in science and engineering.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


