剥离序列
IF 0.6
3区 数学
Q4 COMPUTER SCIENCE, THEORY & METHODS
引用次数: 0
摘要
给定平面内一般位置的 n 个标记点集合,我们逐个删除其所有点。每移去一个点,就会从剩余集合的凸壳中移除一个点。这个过程有多少种方式?答案显然取决于点集。如果点都在凸面位置,那么正好有 n 种方法,这是 n 个点的最大方法数。那么最小的路数是多少呢?结果表明,这个数目(大致)至少是(3^n\),最多是(12.29^n\)。本文章由计算机程序翻译,如有差异,请以英文原文为准。
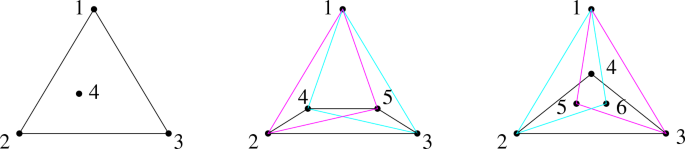
Peeling Sequences
Given a set of n labeled points in general position in the plane, we remove all of its points one by one. At each step, one point from the convex hull of the remaining set is erased. In how many ways can the process be carried out? The answer obviously depends on the point set. If the points are in convex position, there are exactly n! ways, which is the maximum number of ways for n points. But what is the minimum number? It is shown that this number is (roughly) at least \(3^n\) and at most \(12.29^n\).
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Discrete & Computational Geometry
数学-计算机:理论方法
CiteScore
1.80
自引率
12.50%
发文量
99
审稿时长
6-12 weeks
期刊介绍:
Discrete & Computational Geometry (DCG) is an international journal of mathematics and computer science, covering a broad range of topics in which geometry plays a fundamental role. It publishes papers on such topics as configurations and arrangements, spatial subdivision, packing, covering, and tiling, geometric complexity, polytopes, point location, geometric probability, geometric range searching, combinatorial and computational topology, probabilistic techniques in computational geometry, geometric graphs, geometry of numbers, and motion planning.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


