On the existence of a nodal solution for p-Laplacian equations depending on the gradient

In the present paper we deal with a quasi-linear elliptic equation depending on a sublinear nonlinearity involving the gradient. We prove the existence of a nontrivial nodal solution employing the theory of invariant sets of descending flow together with sub-supersolution techniques, gradient regularity arguments, strong comparison principle for the $p$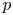-Laplace operator. The same conclusion is obtained for an eigenvalue problem under a different set of assumptions.