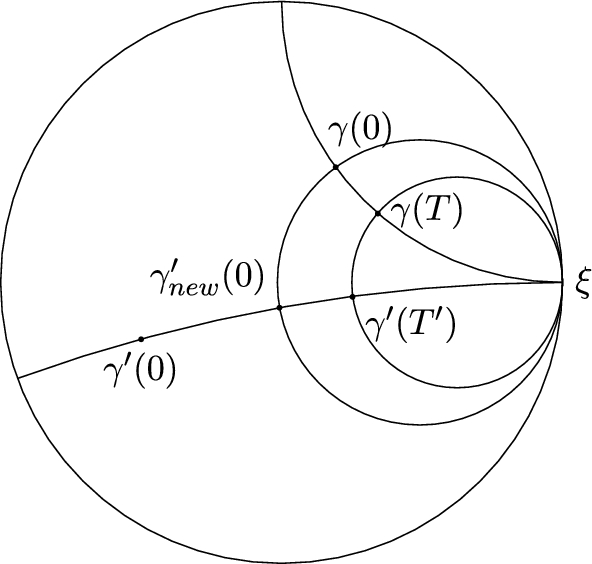
Circumcenter extension maps for non-positively curved spaces

We show that every cross ratio preserving homeomorphism between boundaries of Hadamard manifolds extends to a map, called circumcenter extension, provided that the manifolds satisfy certain visibility conditions. We describe regions on which this map is Hölder-continuous. Furthermore, we show that this map is a rough isometry, whenever the manifolds admit cocompact group actions by isometries and we improve previously known quasi-isometry constants, provided by Biswas, in the case of 2-dimensional \(\mathrm {CAT(-1)}\) manifolds. Finally, we provide a sufficient condition for this map to be an isometry in the case of Hadamard surfaces.