The fully parabolic multi-species chemotaxis system in

This article is devoted to the analysis of the parabolic–parabolic chemotaxis system with multi-components over 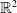$\mathbb{R}^2$. The optimal small initial condition on the global existence of solutions for multi-species chemotaxis model in the fully parabolic situation had not been attained as far as the author knows. In this paper, we prove that under the sub-critical mass condition, any solutions to conflict-free system exist globally. Moreover, the global existence of solutions to system with strong self-repelling effect has been discussed even for large initial data. The proof is based on the modified free energy functional and the Moser–Trudinger inequality for system.