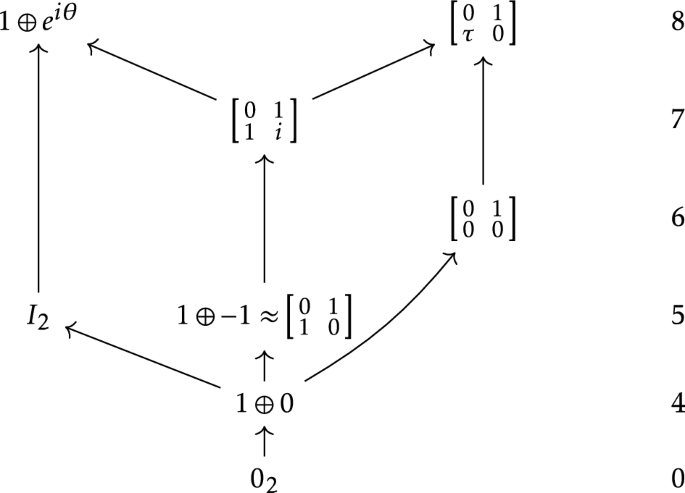
On structures of normal forms of complex points of small $${\mathcal {C}}^{2}$$ -perturbations of real 4-manifolds embedded in a complex 3-manifold

We extend our previous result on the behaviour of the quadratic part of a complex points of a small \({\mathcal {C}}^{2}\)-perturbation of a real 4-manifold embedded in a complex 3-manifold. We describe the change of the structure of the quadratic normal form of a complex point. It is an immediate consequence of a theorem clarifying how small perturbations can change the bundle of a pair of one arbitrary and one symmetric \(2\times 2\) matrix with respect to an action of a certain linear group.