流体层平面和轴对称流动的水力跳动

IF 1 4区物理与天体物理 Q3 PHYSICS, MULTIDISCIPLINARY

Journal of Experimental and Theoretical Physics Pub Date : 2024-01-12 DOI:10.1134/S1063776123110110

A. D. Sukhov, A. G. Petrov

{"title":"流体层平面和轴对称流动的水力跳动","authors":"A. D. Sukhov, A. G. Petrov","doi":"10.1134/S1063776123110110","DOIUrl":null,"url":null,"abstract":"We consider fluid flow with a free boundary, which is defined as a function of height from coordinate x with two asymptotes at positive and negative infinities (hydraulic jump). The Boussinesq approximation is used to describe the phenomenon, and an additional force is introduced. The force is chosen to depend only on the height of the surface. The problem is solved analytically without using numerical schemes. This technique is used to determine the jump surface and the acting force depending on the wave propagation coordinate.","PeriodicalId":629,"journal":{"name":"Journal of Experimental and Theoretical Physics","volume":"137 5","pages":"725 - 731"},"PeriodicalIF":1.0000,"publicationDate":"2024-01-12","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Hydraulic Jump for Planar and Axisymmetric Flow of a Fluid Layer\",\"authors\":\"A. D. Sukhov, A. G. Petrov\",\"doi\":\"10.1134/S1063776123110110\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We consider fluid flow with a free boundary, which is defined as a function of height from coordinate x with two asymptotes at positive and negative infinities (hydraulic jump). The Boussinesq approximation is used to describe the phenomenon, and an additional force is introduced. The force is chosen to depend only on the height of the surface. The problem is solved analytically without using numerical schemes. This technique is used to determine the jump surface and the acting force depending on the wave propagation coordinate.\",\"PeriodicalId\":629,\"journal\":{\"name\":\"Journal of Experimental and Theoretical Physics\",\"volume\":\"137 5\",\"pages\":\"725 - 731\"},\"PeriodicalIF\":1.0000,\"publicationDate\":\"2024-01-12\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Experimental and Theoretical Physics\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://link.springer.com/article/10.1134/S1063776123110110\",\"RegionNum\":4,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"PHYSICS, MULTIDISCIPLINARY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Experimental and Theoretical Physics","FirstCategoryId":"101","ListUrlMain":"https://link.springer.com/article/10.1134/S1063776123110110","RegionNum":4,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"PHYSICS, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

摘要

摘要我们考虑了具有自由边界的流体流动，自由边界被定义为坐标 x 高度的函数，在正无穷大和负无穷大处有两个渐近线（水力跃迁）。我们采用布森斯克近似来描述这一现象，并引入了一个附加力。该力只取决于表面的高度。该问题采用分析方法求解，不使用数值方案。该技术用于确定跃迁面以及取决于波传播坐标的作用力。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

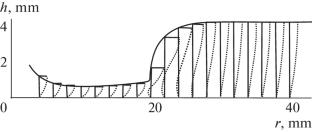
Hydraulic Jump for Planar and Axisymmetric Flow of a Fluid Layer

查看原文本刊更多论文

Hydraulic Jump for Planar and Axisymmetric Flow of a Fluid Layer

We consider fluid flow with a free boundary, which is defined as a function of height from coordinate x with two asymptotes at positive and negative infinities (hydraulic jump). The Boussinesq approximation is used to describe the phenomenon, and an additional force is introduced. The force is chosen to depend only on the height of the surface. The problem is solved analytically without using numerical schemes. This technique is used to determine the jump surface and the acting force depending on the wave propagation coordinate.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Experimental and Theoretical Physics 物理-物理：综合

CiteScore

1.90

自引率

9.10%

发文量

130

审稿时长

3-6 weeks

期刊介绍： Journal of Experimental and Theoretical Physics is one of the most influential physics research journals. Originally based on Russia, this international journal now welcomes manuscripts from all countries in the English or Russian language. It publishes original papers on fundamental theoretical and experimental research in all fields of physics: from solids and liquids to elementary particles and astrophysics.