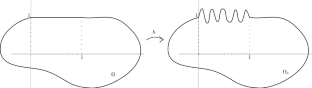
Rate of convergence for reaction–diffusion equations with nonlinear Neumann boundary conditions and $${\mathcal {C}}^1$$ variation of the domain

In this paper, we propose the compact convergence approach to deal with the continuity of attractors of some reaction–diffusion equations under smooth perturbations of the domain subject to nonlinear Neumann boundary conditions. We define a family of invertible linear operators to compare the dynamics of perturbed and unperturbed problems in the same phase space. All continuity arising from small smooth perturbations will be estimated by a rate of convergence given by the domain variation in a \({\mathcal {C}}^1\) topology.