用切比雪夫插值法解决具有恒定延迟的斯特姆-利乌维尔逆问题

IF 1.9 4区数学 Q1 MATHEMATICS

Mathematical Sciences Pub Date : 2024-01-02 DOI:10.1007/s40096-023-00520-5

A. Dabbaghian, S. Akbarpoor Kiasary, H. Koyunbakan, B. Agheli

{"title":"用切比雪夫插值法解决具有恒定延迟的斯特姆-利乌维尔逆问题","authors":"A. Dabbaghian, S. Akbarpoor Kiasary, H. Koyunbakan, B. Agheli","doi":"10.1007/s40096-023-00520-5","DOIUrl":null,"url":null,"abstract":"<p>The inverse nodal problem for Sturm–Liouville operator with a constant delay has been investigated in the present paper. To do so, we have computed the nodal points and nodal lengths. Therefore, we have tried Chebyshev interpolation technique (CIT) to obtain the numerical solution of inverse nodal problem. Following that, a number of numerical examples have been given. The numerical calculations in the present paper have been conducted via pc applying some programs encoded in Matlab software.</p>","PeriodicalId":48563,"journal":{"name":"Mathematical Sciences","volume":"33 2 1","pages":""},"PeriodicalIF":1.9000,"publicationDate":"2024-01-02","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Solving inverse Sturm–Liouville problem featuring a constant delay by Chebyshev interpolation method\",\"authors\":\"A. Dabbaghian, S. Akbarpoor Kiasary, H. Koyunbakan, B. Agheli\",\"doi\":\"10.1007/s40096-023-00520-5\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>The inverse nodal problem for Sturm–Liouville operator with a constant delay has been investigated in the present paper. To do so, we have computed the nodal points and nodal lengths. Therefore, we have tried Chebyshev interpolation technique (CIT) to obtain the numerical solution of inverse nodal problem. Following that, a number of numerical examples have been given. The numerical calculations in the present paper have been conducted via pc applying some programs encoded in Matlab software.</p>\",\"PeriodicalId\":48563,\"journal\":{\"name\":\"Mathematical Sciences\",\"volume\":\"33 2 1\",\"pages\":\"\"},\"PeriodicalIF\":1.9000,\"publicationDate\":\"2024-01-02\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Mathematical Sciences\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s40096-023-00520-5\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Mathematical Sciences","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s40096-023-00520-5","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

本文研究了具有恒定延迟的 Sturm-Liouville 算子的反节点问题。为此，我们计算了节点点和节点长度。因此，我们尝试了切比雪夫插值技术（CIT）来获得反节点问题的数值解。随后，我们给出了一些数值示例。本文中的数值计算是通过 PC 机应用 Matlab 软件中的一些程序进行的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

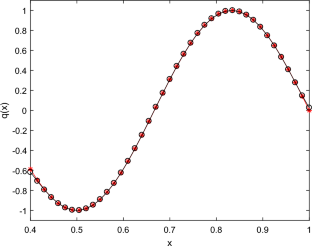
Solving inverse Sturm–Liouville problem featuring a constant delay by Chebyshev interpolation method

查看原文本刊更多论文

Solving inverse Sturm–Liouville problem featuring a constant delay by Chebyshev interpolation method

The inverse nodal problem for Sturm–Liouville operator with a constant delay has been investigated in the present paper. To do so, we have computed the nodal points and nodal lengths. Therefore, we have tried Chebyshev interpolation technique (CIT) to obtain the numerical solution of inverse nodal problem. Following that, a number of numerical examples have been given. The numerical calculations in the present paper have been conducted via pc applying some programs encoded in Matlab software.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Mathematical Sciences Multiple-

CiteScore

4.20

自引率

5.00%

发文量

期刊介绍： Mathematical Sciences is an international journal publishing high quality peer-reviewed original research articles that demonstrate the interaction between various disciplines of theoretical and applied mathematics. Subject areas include numerical analysis, numerical statistics, optimization, operational research, signal analysis, wavelets, image processing, fuzzy sets, spline, stochastic analysis, integral equation, differential equation, partial differential equation and combinations of the above.