装饰 AKLT 模型的光谱间隙稳定性和基态可分辨性

IF 1.4 3区物理与天体物理 Q2 PHYSICS, MATHEMATICAL

Annales Henri Poincaré Pub Date : 2023-12-27 DOI:10.1007/s00023-023-01398-8

Angelo Lucia, Alvin Moon, Amanda Young

{"title":"装饰 AKLT 模型的光谱间隙稳定性和基态可分辨性","authors":"Angelo Lucia, Alvin Moon, Amanda Young","doi":"10.1007/s00023-023-01398-8","DOIUrl":null,"url":null,"abstract":"<div><p>We use cluster expansion methods to establish local the indistiguishability of the finite volume ground states for the AKLT model on decorated hexagonal lattices with decoration parameter at least 5. Our estimates imply that the model satisfies local topological quantum order, and so, the spectral gap above the ground state is stable against local perturbations.</p></div>","PeriodicalId":463,"journal":{"name":"Annales Henri Poincaré","volume":"25 8","pages":"3603 - 3648"},"PeriodicalIF":1.4000,"publicationDate":"2023-12-27","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://link.springer.com/content/pdf/10.1007/s00023-023-01398-8.pdf","citationCount":"0","resultStr":"{\"title\":\"Stability of the Spectral Gap and Ground State Indistinguishability for a Decorated AKLT Model\",\"authors\":\"Angelo Lucia, Alvin Moon, Amanda Young\",\"doi\":\"10.1007/s00023-023-01398-8\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>We use cluster expansion methods to establish local the indistiguishability of the finite volume ground states for the AKLT model on decorated hexagonal lattices with decoration parameter at least 5. Our estimates imply that the model satisfies local topological quantum order, and so, the spectral gap above the ground state is stable against local perturbations.</p></div>\",\"PeriodicalId\":463,\"journal\":{\"name\":\"Annales Henri Poincaré\",\"volume\":\"25 8\",\"pages\":\"3603 - 3648\"},\"PeriodicalIF\":1.4000,\"publicationDate\":\"2023-12-27\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://link.springer.com/content/pdf/10.1007/s00023-023-01398-8.pdf\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Annales Henri Poincaré\",\"FirstCategoryId\":\"4\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00023-023-01398-8\",\"RegionNum\":3,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"PHYSICS, MATHEMATICAL\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Annales Henri Poincaré","FirstCategoryId":"4","ListUrlMain":"https://link.springer.com/article/10.1007/s00023-023-01398-8","RegionNum":3,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"PHYSICS, MATHEMATICAL","Score":null,"Total":0}

引用次数: 0

摘要

我们使用聚类展开方法确定了装饰参数至少为 5 的装饰六边形晶格上 AKLT 模型有限体积基态的局部不可分割性。我们的估计意味着该模型满足局部拓扑量子秩序，因此基态上方的谱隙在局部扰动下是稳定的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

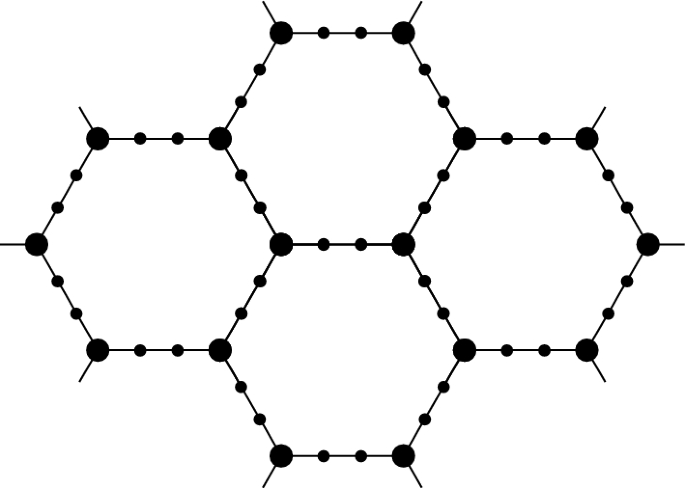
Stability of the Spectral Gap and Ground State Indistinguishability for a Decorated AKLT Model

查看原文本刊更多论文

Stability of the Spectral Gap and Ground State Indistinguishability for a Decorated AKLT Model

We use cluster expansion methods to establish local the indistiguishability of the finite volume ground states for the AKLT model on decorated hexagonal lattices with decoration parameter at least 5. Our estimates imply that the model satisfies local topological quantum order, and so, the spectral gap above the ground state is stable against local perturbations.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Annales Henri Poincaré 物理-物理：粒子与场物理

CiteScore

3.00

自引率

6.70%

发文量

108

审稿时长

6-12 weeks

期刊介绍： The two journals Annales de l''Institut Henri Poincaré, physique théorique and Helvetica Physical Acta merged into a single new journal under the name Annales Henri Poincaré - A Journal of Theoretical and Mathematical Physics edited jointly by the Institut Henri Poincaré and by the Swiss Physical Society. The goal of the journal is to serve the international scientific community in theoretical and mathematical physics by collecting and publishing original research papers meeting the highest professional standards in the field. The emphasis will be on analytical theoretical and mathematical physics in a broad sense.