有感染的捕食者-猎物系统中的霍普夫分岔

IF 0.8 4区数学 Q2 MATHEMATICS

Differential Equations Pub Date : 2023-12-29 DOI:10.1134/s00122661230110125

A. P. Krishchenko, O. A. Podderegin

{"title":"有感染的捕食者-猎物系统中的霍普夫分岔","authors":"A. P. Krishchenko, O. A. Podderegin","doi":"10.1134/s00122661230110125","DOIUrl":null,"url":null,"abstract":"<h3 data-test=\"abstract-sub-heading\">Abstract</h3><p> We study a model of a predator–prey system with possible infection of prey in the form of\na three-dimensional system of ordinary differential equations. Using the localization method of\ncompact invariant sets, the existence of an attractor is proved and a compact positively invariant\nset is found that estimates its position. The conditions for the extinction of populations and the\nexistence of equilibria are found. A numerical method for finding a Hopf bifurcation of the inner\nequilibrium is proposed and an example of an arising stable limit cycle is given.\n</p>","PeriodicalId":50580,"journal":{"name":"Differential Equations","volume":"23 1","pages":""},"PeriodicalIF":0.8000,"publicationDate":"2023-12-29","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Hopf Bifurcation in a Predator–Prey System with Infection\",\"authors\":\"A. P. Krishchenko, O. A. Podderegin\",\"doi\":\"10.1134/s00122661230110125\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<h3 data-test=\\\"abstract-sub-heading\\\">Abstract</h3><p> We study a model of a predator–prey system with possible infection of prey in the form of\\na three-dimensional system of ordinary differential equations. Using the localization method of\\ncompact invariant sets, the existence of an attractor is proved and a compact positively invariant\\nset is found that estimates its position. The conditions for the extinction of populations and the\\nexistence of equilibria are found. A numerical method for finding a Hopf bifurcation of the inner\\nequilibrium is proposed and an example of an arising stable limit cycle is given.\\n</p>\",\"PeriodicalId\":50580,\"journal\":{\"name\":\"Differential Equations\",\"volume\":\"23 1\",\"pages\":\"\"},\"PeriodicalIF\":0.8000,\"publicationDate\":\"2023-12-29\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Differential Equations\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1134/s00122661230110125\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Differential Equations","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1134/s00122661230110125","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

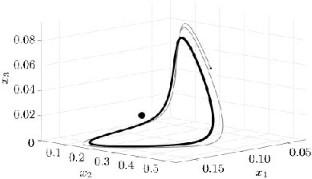
摘要我们以一个三维常微分方程系统的形式研究了一个捕食者--猎物系统模型，其中猎物可能受到感染。利用紧凑不变集的定位方法，证明了吸引子的存在，并找到了估计其位置的紧凑正不变集。找到了种群灭绝和均衡存在的条件。提出了寻找非平衡的霍普夫分岔的数值方法，并给出了一个产生稳定极限循环的例子。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

Hopf Bifurcation in a Predator–Prey System with Infection

查看原文本刊更多论文

Hopf Bifurcation in a Predator–Prey System with Infection

Abstract

We study a model of a predator–prey system with possible infection of prey in the form of a three-dimensional system of ordinary differential equations. Using the localization method of compact invariant sets, the existence of an attractor is proved and a compact positively invariant set is found that estimates its position. The conditions for the extinction of populations and the existence of equilibria are found. A numerical method for finding a Hopf bifurcation of the inner equilibrium is proposed and an example of an arising stable limit cycle is given.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Differential Equations 数学-数学

CiteScore

1.30

自引率

33.30%

发文量

审稿时长

3-8 weeks

期刊介绍： Differential Equations is a journal devoted to differential equations and the associated integral equations. The journal publishes original articles by authors from all countries and accepts manuscripts in English and Russian. The topics of the journal cover ordinary differential equations, partial differential equations, spectral theory of differential operators, integral and integral–differential equations, difference equations and their applications in control theory, mathematical modeling, shell theory, informatics, and oscillation theory. The journal is published in collaboration with the Department of Mathematics and the Division of Nanotechnologies and Information Technologies of the Russian Academy of Sciences and the Institute of Mathematics of the National Academy of Sciences of Belarus.