凸四边形中与方向有关的弦长分布
IF 0.4
4区 数学
Q4 MATHEMATICS
Journal of Contemporary Mathematical Analysis-Armenian Academy of Sciences
Pub Date : 2023-12-28
DOI:10.3103/s1068362323060055
引用次数: 0
摘要
摘要 这项研究致力于通过凸体低维截面的概率特征识别凸体。本文引入了任意凸四边形的五个与方向相关的特征,并对每个方向进行了明确评估。根据这些特征,不仅为任意凸四边形,而且为基于该四边形的任何右棱柱,获得了与方向相关的弦长分布函数和协方差图的简单明确表示。本文章由计算机程序翻译,如有差异,请以英文原文为准。
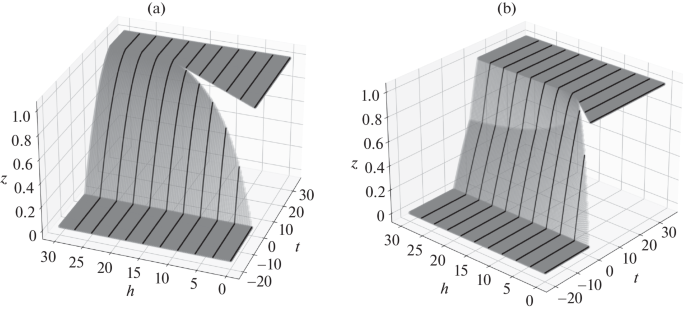
Orientation-Dependent Chord Length Distribution in a Convex Quadrilateral
Abstract
This work contributes to the research devoted to the recognition of a convex body by probabilistic characteristics of its lower-dimensional sections. In this paper, for any convex quadrilateral, five orientation-dependent characteristics are introduced and explicitly evaluated per direction. In terms of these characteristics, simple explicit representations of the orientation-dependent chord length distribution function and the covariogram are obtained not only for an arbitrary convex quadrilateral but also for any right prism based on it.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
0.70
自引率
0.00%
发文量
32
审稿时长
>12 weeks
期刊介绍:
Journal of Contemporary Mathematical Analysis (Armenian Academy of Sciences) is an outlet for research stemming from the widely acclaimed Armenian school of theory of functions, this journal today continues the traditions of that school in the area of general analysis. A very prolific group of mathematicians in Yerevan contribute to this leading mathematics journal in the following fields: real and complex analysis; approximations; boundary value problems; integral and stochastic geometry; differential equations; probability; integral equations; algebra.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


