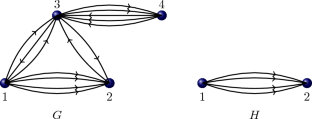
On the \({A_{\!\mathbb {C}}}\)-rank of multidigraphs

The complex adjacency matrix \({A_{\!\mathbb {C}}}(G)\) for a multidigraph G is introduced in Barik and Sahoo (AKCE Int J Graphs Comb 17(1):466–479, 2020). We study the rank of multidigraphs corresponding to the complex adjacency matrix and call it \({A_{\!\mathbb {C}}}\)-rank. It is known that a connected graph G has rank 2 if and only if G is a complete bipartite graph, and has rank 3 if and only if it is a complete tripartite graph (Cheng in Electron J Linear Algebra 16:60–67, 2007). We observe that these results hold as special cases for multidigraphs but are not sufficient. In this article, we characterize all multidigraphs with \({A_{\!\mathbb {C}}}\)-rank 2 and 3, respectively.