Prenex 标准化和公式的分层分类

IF 0.3 4区数学 Q1 Arts and Humanities

Archive for Mathematical Logic Pub Date : 2023-12-23 DOI:10.1007/s00153-023-00899-x

Makoto Fujiwara, Taishi Kurahashi

{"title":"Prenex 标准化和公式的分层分类","authors":"Makoto Fujiwara, Taishi Kurahashi","doi":"10.1007/s00153-023-00899-x","DOIUrl":null,"url":null,"abstract":"<div>Akama et al. [1] introduced a hierarchical classification of first-order formulas for a hierarchical prenex normal form theorem in semi-classical arithmetic. In this paper, we give a justification for the hierarchical classification in a general context of first-order theories. To this end, we first formalize the standard transformation procedure for prenex normalization. Then we show that the classes \\(\\textrm{E}_k\\) and \\(\\textrm{U}_k\\) introduced in [1] are exactly the classes induced by \\(\\Sigma _k\\) and \\(\\Pi _k\\) respectively via the transformation procedure in any first-order theory.</div>","PeriodicalId":48853,"journal":{"name":"Archive for Mathematical Logic","volume":null,"pages":null},"PeriodicalIF":0.3000,"publicationDate":"2023-12-23","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Prenex normalization and the hierarchical classification of formulas\",\"authors\":\"Makoto Fujiwara, Taishi Kurahashi\",\"doi\":\"10.1007/s00153-023-00899-x\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div>Akama et al. [1] introduced a hierarchical classification of first-order formulas for a hierarchical prenex normal form theorem in semi-classical arithmetic. In this paper, we give a justification for the hierarchical classification in a general context of first-order theories. To this end, we first formalize the standard transformation procedure for prenex normalization. Then we show that the classes \\\\(\\\\textrm{E}_k\\\\) and \\\\(\\\\textrm{U}_k\\\\) introduced in [1] are exactly the classes induced by \\\\(\\\\Sigma _k\\\\) and \\\\(\\\\Pi _k\\\\) respectively via the transformation procedure in any first-order theory.</div>\",\"PeriodicalId\":48853,\"journal\":{\"name\":\"Archive for Mathematical Logic\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.3000,\"publicationDate\":\"2023-12-23\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Archive for Mathematical Logic\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00153-023-00899-x\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"Arts and Humanities\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Archive for Mathematical Logic","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s00153-023-00899-x","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"Arts and Humanities","Score":null,"Total":0}

引用次数: 0

摘要

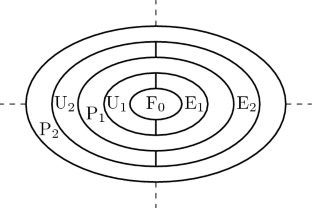
Akama 等人[1]针对半经典算术中的分层前附件正则表达式定理，提出了一阶公式的分层分类法。在本文中，我们在一阶理论的一般背景下给出了分层分类的理由。为此，我们首先形式化了前附件正常化的标准转换过程。然后，我们证明[1]中引入的类\(textrm{E}_k\) 和\(textrm{U}_k\)正是在任何一阶理论中通过转换过程分别由\(\Sigma _k\) 和\(\Pi _k\)引起的类。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

Prenex normalization and the hierarchical classification of formulas

查看原文本刊更多论文

Prenex normalization and the hierarchical classification of formulas

Akama et al. [1] introduced a hierarchical classification of first-order formulas for a hierarchical prenex normal form theorem in semi-classical arithmetic. In this paper, we give a justification for the hierarchical classification in a general context of first-order theories. To this end, we first formalize the standard transformation procedure for prenex normalization. Then we show that the classes \(\textrm{E}_k\) and \(\textrm{U}_k\) introduced in [1] are exactly the classes induced by \(\Sigma _k\) and \(\Pi _k\) respectively via the transformation procedure in any first-order theory.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Archive for Mathematical Logic MATHEMATICS-LOGIC

CiteScore

0.80

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： The journal publishes research papers and occasionally surveys or expositions on mathematical logic. Contributions are also welcomed from other related areas, such as theoretical computer science or philosophy, as long as the methods of mathematical logic play a significant role. The journal therefore addresses logicians and mathematicians, computer scientists, and philosophers who are interested in the applications of mathematical logic in their own field, as well as its interactions with other areas of research.