正则图中的边连接性和成对不相交完全匹配

IF 1 2区数学 Q1 MATHEMATICS

Combinatorica Pub Date : 2023-12-19 DOI:10.1007/s00493-023-00078-9

Yulai Ma, Davide Mattiolo, Eckhard Steffen, Isaak H. Wolf

{"title":"正则图中的边连接性和成对不相交完全匹配","authors":"Yulai Ma, Davide Mattiolo, Eckhard Steffen, Isaak H. Wolf","doi":"10.1007/s00493-023-00078-9","DOIUrl":null,"url":null,"abstract":"For \\(0 \\le t \\le r\\) let m(t, r) be the maximum number s such that every t-edge-connected r-graph has s pairwise disjoint perfect matchings. There are only a few values of m(t, r) known, for instance \\(m(3,3)=m(4,r)=1\\), and \\(m(t,r) \\le r-2\\) for all \\(t \\not = 5\\), and \\(m(t,r) \\le r-3\\) if r is even. We prove that \\(m(2l,r) \\le 3l - 6\\) for every \\(l \\ge 3\\) and \\(r \\ge 2 l\\).","PeriodicalId":50666,"journal":{"name":"Combinatorica","volume":"38 1","pages":""},"PeriodicalIF":1.0000,"publicationDate":"2023-12-19","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Edge-Connectivity and Pairwise Disjoint Perfect Matchings in Regular Graphs\",\"authors\":\"Yulai Ma, Davide Mattiolo, Eckhard Steffen, Isaak H. Wolf\",\"doi\":\"10.1007/s00493-023-00078-9\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"For \\\\(0 \\\\le t \\\\le r\\\\) let m(t, r) be the maximum number s such that every t-edge-connected r-graph has s pairwise disjoint perfect matchings. There are only a few values of m(t, r) known, for instance \\\\(m(3,3)=m(4,r)=1\\\\), and \\\\(m(t,r) \\\\le r-2\\\\) for all \\\\(t \\\\not = 5\\\\), and \\\\(m(t,r) \\\\le r-3\\\\) if r is even. We prove that \\\\(m(2l,r) \\\\le 3l - 6\\\\) for every \\\\(l \\\\ge 3\\\\) and \\\\(r \\\\ge 2 l\\\\).\",\"PeriodicalId\":50666,\"journal\":{\"name\":\"Combinatorica\",\"volume\":\"38 1\",\"pages\":\"\"},\"PeriodicalIF\":1.0000,\"publicationDate\":\"2023-12-19\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Combinatorica\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00493-023-00078-9\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Combinatorica","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00493-023-00078-9","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

对于（0 \le t \le r\），让 m(t, r) 是最大的数 s，使得每个 t 边连接的 r 图都有 s 个成双成对的完美匹配。m(t,r)只有少数几个已知值，例如：（m(3,3)=m(4,r)=1），在所有（t不=5）的情况下（m(t,r) （le r-2），如果r是偶数，则（m(t,r) （le r-3）。我们证明，对于每一个l和r来说，m（2l,r）都是3l-6。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

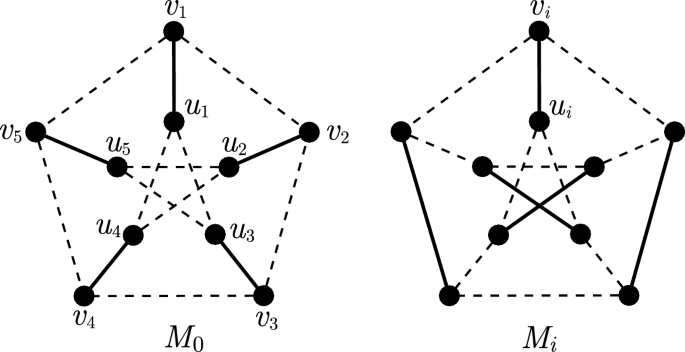
Edge-Connectivity and Pairwise Disjoint Perfect Matchings in Regular Graphs

查看原文本刊更多论文

Edge-Connectivity and Pairwise Disjoint Perfect Matchings in Regular Graphs

For \(0 \le t \le r\) let m(t, r) be the maximum number s such that every t-edge-connected r-graph has s pairwise disjoint perfect matchings. There are only a few values of m(t, r) known, for instance \(m(3,3)=m(4,r)=1\), and \(m(t,r) \le r-2\) for all \(t \not = 5\), and \(m(t,r) \le r-3\) if r is even. We prove that \(m(2l,r) \le 3l - 6\) for every \(l \ge 3\) and \(r \ge 2 l\).

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Combinatorica 数学-数学

CiteScore

1.90

自引率

0.00%

发文量

审稿时长

>12 weeks

期刊介绍： COMBINATORICA publishes research papers in English in a variety of areas of combinatorics and the theory of computing, with particular emphasis on general techniques and unifying principles. Typical but not exclusive topics covered by COMBINATORICA are - Combinatorial structures (graphs, hypergraphs, matroids, designs, permutation groups). - Combinatorial optimization. - Combinatorial aspects of geometry and number theory. - Algorithms in combinatorics and related fields. - Computational complexity theory. - Randomization and explicit construction in combinatorics and algorithms.