赫德涅米等价空间猜想的拓扑版本
IF 1
2区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
著名的赫德涅米猜想的拓扑版本是这样说的两个 \({\mathbb {Z}}/2\)- 空间的笛卡尔积的映射指数等于它们的 \({\mathbb {Z}}/2\)- 指数的最小值。本文的主要目的是研究 G 空间的赫德涅米猜想的拓扑版本。事实上,我们证明了拓扑的赫德涅米猜想对于一般的 G 空间对是不成立的。更准确地说,我们证明了如果 G 群是循环 p 群或大小为 2 的幂的广义四元数群,这个猜想就有可能成立。本文章由计算机程序翻译,如有差异,请以英文原文为准。
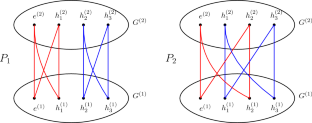
A Topological Version of Hedetniemi’s Conjecture for Equivariant Spaces
A topological version of the famous Hedetniemi conjecture says: The mapping index of the Cartesian product of two \({\mathbb {Z}}/2\)- spaces is equal to the minimum of their \({\mathbb {Z}}/2\)-indexes. The main purpose of this article is to study the topological version of the Hedetniemi conjecture for G-spaces. Indeed, we show that the topological Hedetniemi conjecture cannot be valid for general pairs of G-spaces. More precisely, we show that this conjecture can possibly survive if the group G is either a cyclic p-group or a generalized quaternion group whose size is a power of 2.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Combinatorica
数学-数学
CiteScore
1.90
自引率
0.00%
发文量
45
审稿时长
>12 weeks
期刊介绍:
COMBINATORICA publishes research papers in English in a variety of areas of combinatorics and the theory of computing, with particular emphasis on general techniques and unifying principles. Typical but not exclusive topics covered by COMBINATORICA are
- Combinatorial structures (graphs, hypergraphs, matroids, designs, permutation groups).
- Combinatorial optimization.
- Combinatorial aspects of geometry and number theory.
- Algorithms in combinatorics and related fields.
- Computational complexity theory.
- Randomization and explicit construction in combinatorics and algorithms.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


