通过埃奇沃斯扩展修正点功率变化估计器

IF 0.9 4区数学 Q3 STATISTICS & PROBABILITY

Metrika Pub Date : 2023-12-18 DOI:10.1007/s00184-023-00935-z

Lidan He, Qiang Liu, Zhi Liu, Andrea Bucci

{"title":"通过埃奇沃斯扩展修正点功率变化估计器","authors":"Lidan He, Qiang Liu, Zhi Liu, Andrea Bucci","doi":"10.1007/s00184-023-00935-z","DOIUrl":null,"url":null,"abstract":"<p>In this paper, we propose an estimator of power spot volatility of order p through Edgeworth expansion. We provide a precise description of how to compute the expansion and the first four cumulants are given in an explicit form. We also construct feasible confidence intervals (one-sided and two-sided) for the pth power spot volatility estimator by using Edgeworth expansion. A Monte Carlo simulation study shows that the confidence intervals and probability density curve based on Edgeworth expansion perform better than the conventional case based on Normal approximation.\n</p>","PeriodicalId":49821,"journal":{"name":"Metrika","volume":"242 1","pages":""},"PeriodicalIF":0.9000,"publicationDate":"2023-12-18","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Correcting spot power variation estimator via Edgeworth expansion\",\"authors\":\"Lidan He, Qiang Liu, Zhi Liu, Andrea Bucci\",\"doi\":\"10.1007/s00184-023-00935-z\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>In this paper, we propose an estimator of power spot volatility of order p through Edgeworth expansion. We provide a precise description of how to compute the expansion and the first four cumulants are given in an explicit form. We also construct feasible confidence intervals (one-sided and two-sided) for the pth power spot volatility estimator by using Edgeworth expansion. A Monte Carlo simulation study shows that the confidence intervals and probability density curve based on Edgeworth expansion perform better than the conventional case based on Normal approximation.\\n</p>\",\"PeriodicalId\":49821,\"journal\":{\"name\":\"Metrika\",\"volume\":\"242 1\",\"pages\":\"\"},\"PeriodicalIF\":0.9000,\"publicationDate\":\"2023-12-18\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Metrika\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00184-023-00935-z\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"STATISTICS & PROBABILITY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Metrika","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00184-023-00935-z","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"STATISTICS & PROBABILITY","Score":null,"Total":0}

引用次数: 0

摘要

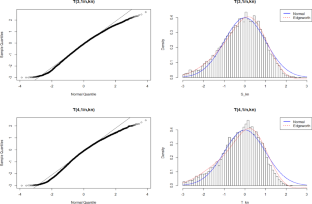
在本文中，我们提出了一种通过埃奇沃斯扩展估算 p 阶幂级数现货波动率的方法。我们提供了如何计算扩展的精确描述，并以明确的形式给出了前四个累积量。我们还利用埃奇沃斯扩展为 pth 幂现货波动率估计值构建了可行的置信区间（单边和双边）。蒙特卡罗模拟研究表明，基于埃奇沃斯扩展的置信区间和概率密度曲线比基于正态近似的传统情况表现更好。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

Correcting spot power variation estimator via Edgeworth expansion

查看原文本刊更多论文

Correcting spot power variation estimator via Edgeworth expansion

In this paper, we propose an estimator of power spot volatility of order p through Edgeworth expansion. We provide a precise description of how to compute the expansion and the first four cumulants are given in an explicit form. We also construct feasible confidence intervals (one-sided and two-sided) for the pth power spot volatility estimator by using Edgeworth expansion. A Monte Carlo simulation study shows that the confidence intervals and probability density curve based on Edgeworth expansion perform better than the conventional case based on Normal approximation.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Metrika 数学-统计学与概率论

CiteScore

1.50

自引率

14.30%

发文量

审稿时长

6-12 weeks

期刊介绍： Metrika is an international journal for theoretical and applied statistics. Metrika publishes original research papers in the field of mathematical statistics and statistical methods. Great importance is attached to new developments in theoretical statistics, statistical modeling and to actual innovative applicability of the proposed statistical methods and results. Topics of interest include, without being limited to, multivariate analysis, high dimensional statistics and nonparametric statistics; categorical data analysis and latent variable models; reliability, lifetime data analysis and statistics in engineering sciences.