具有固定间隔交换变换的关系

IF 0.5 4区数学 Q3 MATHEMATICS

Geometriae Dedicata Pub Date : 2023-12-15 DOI:10.1007/s10711-023-00868-x

Magali Jay

{"title":"具有固定间隔交换变换的关系","authors":"Magali Jay","doi":"10.1007/s10711-023-00868-x","DOIUrl":null,"url":null,"abstract":"<h3>Abstract</h3> We study the group of all interval exchange transformations (IETs). Katok asked whether it contains a free subgroup. We show that for every IET S, there exists a dense open set \\(\\Omega (S)\\) of admissible IETs such that the group generated by S and any \\(T\\in \\Omega (S)\\) is not free of rank 2. This extends a result by Dahmani et al. (Groups Geom Dyn 7(4):883–910, 2013): the group generated by a generic pair of elements of IET([0;1)) is not free (assuming a suitable condition on the underlying permutation).","PeriodicalId":55103,"journal":{"name":"Geometriae Dedicata","volume":"295 2 1","pages":""},"PeriodicalIF":0.5000,"publicationDate":"2023-12-15","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Relations with a fixed interval exchange transformation\",\"authors\":\"Magali Jay\",\"doi\":\"10.1007/s10711-023-00868-x\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<h3>Abstract</h3> We study the group of all interval exchange transformations (IETs). Katok asked whether it contains a free subgroup. We show that for every IET S, there exists a dense open set \\\\(\\\\Omega (S)\\\\) of admissible IETs such that the group generated by S and any \\\\(T\\\\in \\\\Omega (S)\\\\) is not free of rank 2. This extends a result by Dahmani et al. (Groups Geom Dyn 7(4):883–910, 2013): the group generated by a generic pair of elements of IET([0;1)) is not free (assuming a suitable condition on the underlying permutation).\",\"PeriodicalId\":55103,\"journal\":{\"name\":\"Geometriae Dedicata\",\"volume\":\"295 2 1\",\"pages\":\"\"},\"PeriodicalIF\":0.5000,\"publicationDate\":\"2023-12-15\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Geometriae Dedicata\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s10711-023-00868-x\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Geometriae Dedicata","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s10711-023-00868-x","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

摘要我们研究了所有区间交换变换（IET）群。卡托克问它是否包含一个自由子群。我们证明，对于每一个 IET S，都存在一个可容许 IET 的密集开集 \(\Omega (S)\) ，使得由 S 和任何 \(T\in \Omega (S)\) 生成的群不是秩为 2 的自由群。这扩展了 Dahmani 等人的一个结果（Groups Geom Dyn 7(4):883-910, 2013）：IET([0;1))的一般元素对所生成的群不是自由的（假设对底层置换有合适的条件）。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

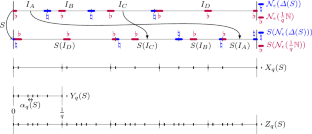
Relations with a fixed interval exchange transformation

查看原文本刊更多论文

Relations with a fixed interval exchange transformation

Abstract

We study the group of all interval exchange transformations (IETs). Katok asked whether it contains a free subgroup. We show that for every IET S, there exists a dense open set \(\Omega (S)\) of admissible IETs such that the group generated by S and any \(T\in \Omega (S)\) is not free of rank 2. This extends a result by Dahmani et al. (Groups Geom Dyn 7(4):883–910, 2013): the group generated by a generic pair of elements of IET([0;1)) is not free (assuming a suitable condition on the underlying permutation).

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Geometriae Dedicata 数学-数学

CiteScore

0.90

自引率

0.00%

发文量

审稿时长

4-8 weeks

期刊介绍： Geometriae Dedicata concentrates on geometry and its relationship to topology, group theory and the theory of dynamical systems. Geometriae Dedicata aims to be a vehicle for excellent publications in geometry and related areas. Features of the journal will include: A fast turn-around time for articles. Special issues centered on specific topics. All submitted papers should include some explanation of the context of the main results. Geometriae Dedicata was founded in 1972 on the initiative of Hans Freudenthal in Utrecht, the Netherlands, who viewed geometry as a method rather than as a field. The present Board of Editors tries to continue in this spirit. The steady growth of the journal since its foundation is witness to the validity of the founder''s vision and to the success of the Editors'' mission.