A Bregman inertial forward-reflected-backward method for nonconvex minimization

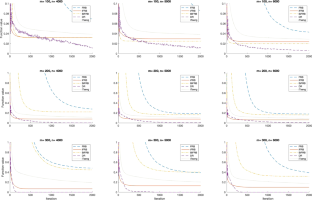
We propose a Bregman inertial forward-reflected-backward (BiFRB) method for nonconvex composite problems. Assuming the generalized concave Kurdyka-Łojasiewicz property, we obtain sequential convergence of BiFRB, as well as convergence rates on both the function value and actual sequence. One distinguishing feature in our analysis is that we utilize a careful treatment of merit function parameters, circumventing the usual restrictive assumption on the inertial parameters. We also present formulae for the Bregman subproblem, supplementing not only BiFRB but also the work of Boţ-Csetnek-László and Boţ-Csetnek. Numerical simulations are conducted to evaluate the performance of our proposed algorithm.