A dynamical classification for crossed products of fiberwise essentially minimal zero-dimensional dynamical systems

We prove that crossed products of fiberwise essentially minimal zero-dimensional dynamical systems, a class that includes systems in which all orbit closures are minimal, have isomorphic K-theory if and only if the dynamical systems are strong orbit equivalent. Under the additional assumption that the dynamical systems have no periodic points, this gives a classification theorem including isomorphism of the associated crossed product 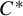$C^*$-algebras as well. We additionally explore the K-theory of such crossed products and the Bratteli diagrams associated to the dynamical systems.