演化p-双拉普拉斯方程的离散化

IF 0.4 Q4 MATHEMATICS, APPLIED

Numerical Analysis and Applications Pub Date : 2022-12-08 DOI:10.1134/s1995423922040036

M. Djaghout, A. Chaoui, K. Zennir

{"title":"演化p-双拉普拉斯方程的离散化","authors":"M. Djaghout, A. Chaoui, K. Zennir","doi":"10.1134/s1995423922040036","DOIUrl":null,"url":null,"abstract":"<h3 data-test=\"abstract-sub-heading\">Abstract</h3><p>This article discusses a mixed finite element method combined with the backward-Euler method to study the hyperbolic <i>p</i>–bi-Laplace equation, where the existence and uniqueness of solution for the discretized problem are shown in Lebesgue and Sobolev spaces. A mixed formulation and an inf-sup condition are then given to prove the well-posedness of the scheme and optimal a priori error estimates for fully discrete schemes are extracted. Finally, a numerical example is given to confirm the theoretical results obtained.</p>","PeriodicalId":43697,"journal":{"name":"Numerical Analysis and Applications","volume":"1 1","pages":""},"PeriodicalIF":0.4000,"publicationDate":"2022-12-08","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"On Discretization of the Evolution p-Bi-Laplace Equation\",\"authors\":\"M. Djaghout, A. Chaoui, K. Zennir\",\"doi\":\"10.1134/s1995423922040036\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<h3 data-test=\\\"abstract-sub-heading\\\">Abstract</h3><p>This article discusses a mixed finite element method combined with the backward-Euler method to study the hyperbolic <i>p</i>–bi-Laplace equation, where the existence and uniqueness of solution for the discretized problem are shown in Lebesgue and Sobolev spaces. A mixed formulation and an inf-sup condition are then given to prove the well-posedness of the scheme and optimal a priori error estimates for fully discrete schemes are extracted. Finally, a numerical example is given to confirm the theoretical results obtained.</p>\",\"PeriodicalId\":43697,\"journal\":{\"name\":\"Numerical Analysis and Applications\",\"volume\":\"1 1\",\"pages\":\"\"},\"PeriodicalIF\":0.4000,\"publicationDate\":\"2022-12-08\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Numerical Analysis and Applications\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://doi.org/10.1134/s1995423922040036\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"MATHEMATICS, APPLIED\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Numerical Analysis and Applications","FirstCategoryId":"1085","ListUrlMain":"https://doi.org/10.1134/s1995423922040036","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"MATHEMATICS, APPLIED","Score":null,"Total":0}

引用次数: 0

摘要

摘要本文讨论了用混合有限元法结合后向欧拉法研究双曲型p -双拉普拉斯方程，在Lebesgue和Sobolev空间中给出了离散问题解的存在唯一性。然后给出了一个混合公式和一个自支撑条件来证明该格式的适定性，并提取了完全离散格式的最优先验误差估计。最后通过数值算例验证了理论结果。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

On Discretization of the Evolution p-Bi-Laplace Equation

查看原文本刊更多论文

On Discretization of the Evolution p-Bi-Laplace Equation

Abstract

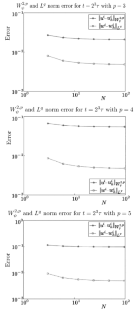
This article discusses a mixed finite element method combined with the backward-Euler method to study the hyperbolic p–bi-Laplace equation, where the existence and uniqueness of solution for the discretized problem are shown in Lebesgue and Sobolev spaces. A mixed formulation and an inf-sup condition are then given to prove the well-posedness of the scheme and optimal a priori error estimates for fully discrete schemes are extracted. Finally, a numerical example is given to confirm the theoretical results obtained.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Numerical Analysis and Applications MATHEMATICS, APPLIED-

CiteScore

1.00

自引率

0.00%

发文量

期刊介绍： Numerical Analysis and Applications is the translation of Russian periodical Sibirskii Zhurnal Vychislitel’noi Matematiki (Siberian Journal of Numerical Mathematics) published by the Siberian Branch of the Russian Academy of Sciences Publishing House since 1998. The aim of this journal is to demonstrate, in concentrated form, to the Russian and International Mathematical Community the latest and most important investigations of Siberian numerical mathematicians in various scientific and engineering fields. The journal deals with the following topics: Theory and practice of computational methods, mathematical physics, and other applied fields; Mathematical models of elasticity theory, hydrodynamics, gas dynamics, and geophysics; Parallelizing of algorithms; Models and methods of bioinformatics.