扩展Snow算法在有限Weyl群中的计算
引用次数: 1
摘要
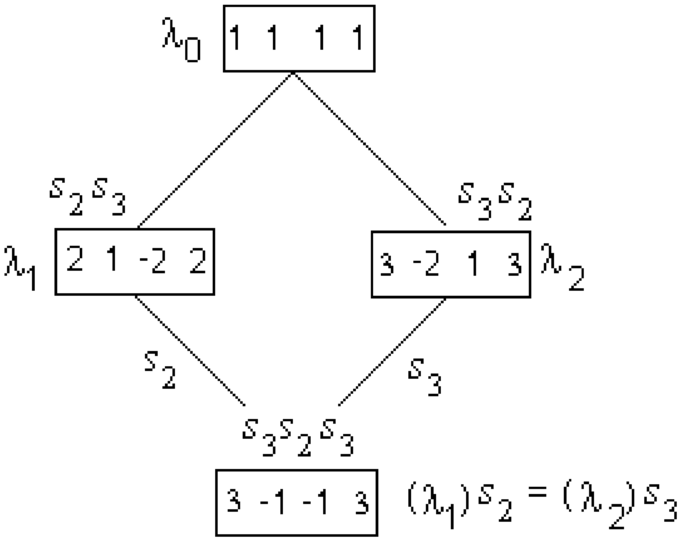
1990年,D. Snow提出了一种计算有限Weyl群轨道的有效算法。Snow的算法是为计算权重、w轨道和Weyl群元素而设计的。提出了对Snow算法的一种扩展,该算法允许在同一运行周期内找到相互逆的元素对并计算w轨道。这简化了Weyl组中共轭类的计算。作为示例,使用扩展的Snow算法获得Weyl组的完整元素列表$W(D_{4})$。$W(D_{4})$的元素以两种方式指定:简化表达式和忠实表示的矩阵。然后我们将这个群划分为共轭类,这些共轭类的元素被指定为简化表达式。给出了$W(D_{4})$共轭类的各种表示形式:带卡特图、带约简表达式和带符号循环类型。在附录中,我们提供了该算法在Python中的实现。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Extending Snow’s algorithm for computations in the finite Weyl groups
In 1990, D. Snow proposed an effective algorithm for computing the orbits of finite Weyl groups. Snow’s algorithm is designed for computation of weights, W-orbits, and elements of the Weyl group. An extension of Snow’s algorithm is proposed, which allows to find pairs of mutually inverse elements together with the calculation of W-orbits in the same runtime cycle. This simplifies the calculation of conjugacy classes in the Weyl group. As an example, the complete list of elements of the Weyl group $W(D_{4})$ obtained using the extended Snow’s algorithm. The elements of $W(D_{4})$ are specified in two ways: as reduced expressions and as matrices of the faithful representation. Then we give a partition of this group into conjugacy classes with elements specified as reduced expressions. Various forms are given for representatives of the conjugacy classes of $W(D_{4})$ : with Carter diagrams, with reduced expressions, and with signed cycle-types. In the Appendix, we provide an implementation of the algorithm in Python.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Fixed Point Theory and Applications
MATHEMATICS, APPLIED-MATHEMATICS
自引率
0.00%
发文量
0
期刊介绍:
In a wide range of mathematical, computational, economical, modeling and engineering problems, the existence of a solution to a theoretical or real world problem is equivalent to the existence of a fixed point for a suitable map or operator. Fixed points are therefore of paramount importance in many areas of mathematics, sciences and engineering.
The theory itself is a beautiful mixture of analysis (pure and applied), topology and geometry. Over the last 60 years or so, the theory of fixed points has been revealed as a very powerful and important tool in the study of nonlinear phenomena. In particular, fixed point techniques have been applied in such diverse fields as biology, chemistry, physics, engineering, game theory and economics.
In numerous cases finding the exact solution is not possible; hence it is necessary to develop appropriate algorithms to approximate the requested result. This is strongly related to control and optimization problems arising in the different sciences and in engineering problems. Many situations in the study of nonlinear equations, calculus of variations, partial differential equations, optimal control and inverse problems can be formulated in terms of fixed point problems or optimization.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


