非周期单面体平铺的周期性衍射。

IF 1.9 4区材料科学 Q3 CHEMISTRY, MULTIDISCIPLINARY

Acta Crystallographica Section A: Foundations and Advances Pub Date : 2024-01-01 DOI:10.1107/S2053273323009506

Craig S Kaplan, Michael O'Keeffe, Michael M J Treacy

{"title":"非周期单面体平铺的周期性衍射。","authors":"Craig S Kaplan, Michael O'Keeffe, Michael M J Treacy","doi":"10.1107/S2053273323009506","DOIUrl":null,"url":null,"abstract":"The diffraction pattern from the recently reported aperiodic `einstein', or `hat', monohedral tiling [Smith et al. (2023). arXiv:2303.10798v1] has been analyzed. The structure is the hexagonal mta net, a kite tiling, with aperiodic vertex deletions. A large model's diffraction pattern displays a robust sixfold periodicity in plane group p6. A repeating, roughly triangular motif of `diffused intensity' arises between the strongest Bragg peaks. The motif contains high-density regions of discrete `satellite' peaks, rather than continuous `diffuse scattering', breaking mirror symmetry, consistent with the chiral hat tiling.","PeriodicalId":106,"journal":{"name":"Acta Crystallographica Section A: Foundations and Advances","volume":" ","pages":"72-78"},"PeriodicalIF":1.9000,"publicationDate":"2024-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Periodic diffraction from an aperiodic monohedral tiling.\",\"authors\":\"Craig S Kaplan, Michael O'Keeffe, Michael M J Treacy\",\"doi\":\"10.1107/S2053273323009506\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"The diffraction pattern from the recently reported aperiodic `einstein', or `hat', monohedral tiling [Smith et al. (2023). arXiv:2303.10798v1] has been analyzed. The structure is the hexagonal mta net, a kite tiling, with aperiodic vertex deletions. A large model's diffraction pattern displays a robust sixfold periodicity in plane group p6. A repeating, roughly triangular motif of `diffused intensity' arises between the strongest Bragg peaks. The motif contains high-density regions of discrete `satellite' peaks, rather than continuous `diffuse scattering', breaking mirror symmetry, consistent with the chiral hat tiling.\",\"PeriodicalId\":106,\"journal\":{\"name\":\"Acta Crystallographica Section A: Foundations and Advances\",\"volume\":\" \",\"pages\":\"72-78\"},\"PeriodicalIF\":1.9000,\"publicationDate\":\"2024-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Acta Crystallographica Section A: Foundations and Advances\",\"FirstCategoryId\":\"1\",\"ListUrlMain\":\"https://doi.org/10.1107/S2053273323009506\",\"RegionNum\":4,\"RegionCategory\":\"材料科学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"CHEMISTRY, MULTIDISCIPLINARY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Acta Crystallographica Section A: Foundations and Advances","FirstCategoryId":"1","ListUrlMain":"https://doi.org/10.1107/S2053273323009506","RegionNum":4,"RegionCategory":"材料科学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"CHEMISTRY, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

摘要

最近报道的非周期性“爱因斯坦”或“帽子”单面体平铺的衍射图样[Smith等人](2023)。[arXiv:2303.10798v1]已分析。结构是六边形的mta网，一个风筝平铺，具有非周期的顶点删除。一个大模型的衍射图样在p6平面群中显示出强大的六倍周期性。在最强的布拉格峰之间出现了一个重复的、大致三角形的“扩散强度”母题。图案包含离散的“卫星”峰的高密度区域，而不是连续的“漫射散射”，打破了镜像对称，与手性帽子平铺一致。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

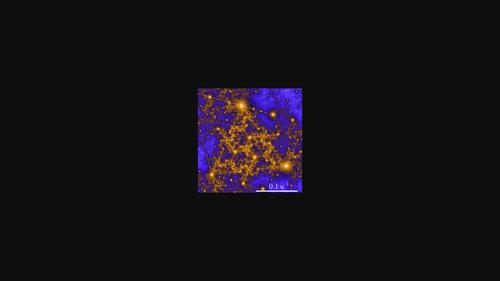
$Periodic diffraction from an aperiodic monohedral tiling.$

查看原文本刊更多论文

Periodic diffraction from an aperiodic monohedral tiling.

The diffraction pattern from the recently reported aperiodic `einstein', or `hat', monohedral tiling [Smith et al. (2023). arXiv:2303.10798v1] has been analyzed. The structure is the hexagonal mta net, a kite tiling, with aperiodic vertex deletions. A large model's diffraction pattern displays a robust sixfold periodicity in plane group p6. A repeating, roughly triangular motif of `diffused intensity' arises between the strongest Bragg peaks. The motif contains high-density regions of discrete `satellite' peaks, rather than continuous `diffuse scattering', breaking mirror symmetry, consistent with the chiral hat tiling.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Acta Crystallographica Section A: Foundations and Advances CHEMISTRY, MULTIDISCIPLINARYCRYSTALLOGRAPH-CRYSTALLOGRAPHY

CiteScore

2.60

自引率

11.10%

发文量

419

期刊介绍： Acta Crystallographica Section A: Foundations and Advances publishes articles reporting advances in the theory and practice of all areas of crystallography in the broadest sense. As well as traditional crystallography, this includes nanocrystals, metacrystals, amorphous materials, quasicrystals, synchrotron and XFEL studies, coherent scattering, diffraction imaging, time-resolved studies and the structure of strain and defects in materials. The journal has two parts, a rapid-publication Advances section and the traditional Foundations section. Articles for the Advances section are of particularly high value and impact. They receive expedited treatment and may be highlighted by an accompanying scientific commentary article and a press release. Further details are given in the November 2013 Editorial. The central themes of the journal are, on the one hand, experimental and theoretical studies of the properties and arrangements of atoms, ions and molecules in condensed matter, periodic, quasiperiodic or amorphous, ideal or real, and, on the other, the theoretical and experimental aspects of the various methods to determine these properties and arrangements.