少数单色有界度图的平铺边彩色图

IF 1 2区数学 Q1 MATHEMATICS

Combinatorica Pub Date : 2023-11-21 DOI:10.1007/s00493-023-00072-1

Jan Corsten, Walner Mendonça

{"title":"少数单色有界度图的平铺边彩色图","authors":"Jan Corsten, Walner Mendonça","doi":"10.1007/s00493-023-00072-1","DOIUrl":null,"url":null,"abstract":"We prove that for all integers \\(\\Delta ,r \\ge 2\\), there is a constant \\(C = C(\\Delta ,r) >0\\) such that the following is true for every sequence \\({\\mathcal {F}}= \\{F_1, F_2, \\ldots \\}\\) of graphs with \\(v(F_n) = n\\) and \\(\\Delta (F_n) \\le \\Delta \\), for each \\(n \\in {\\mathbb {N}}\\). In every r-edge-coloured \\(K_n\\), there is a collection of at most C monochromatic copies from \\({\\mathcal {F}}\\) whose vertex-sets partition \\(V(K_n)\\). This makes progress on a conjecture of Grinshpun and Sárközy.","PeriodicalId":50666,"journal":{"name":"Combinatorica","volume":"27 20","pages":""},"PeriodicalIF":1.0000,"publicationDate":"2023-11-21","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"2","resultStr":"{\"title\":\"Tiling Edge-Coloured Graphs with Few Monochromatic Bounded-Degree Graphs\",\"authors\":\"Jan Corsten, Walner Mendonça\",\"doi\":\"10.1007/s00493-023-00072-1\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We prove that for all integers \\\\(\\\\Delta ,r \\\\ge 2\\\\), there is a constant \\\\(C = C(\\\\Delta ,r) >0\\\\) such that the following is true for every sequence \\\\({\\\\mathcal {F}}= \\\\{F_1, F_2, \\\\ldots \\\\}\\\\) of graphs with \\\\(v(F_n) = n\\\\) and \\\\(\\\\Delta (F_n) \\\\le \\\\Delta \\\\), for each \\\\(n \\\\in {\\\\mathbb {N}}\\\\). In every r-edge-coloured \\\\(K_n\\\\), there is a collection of at most C monochromatic copies from \\\\({\\\\mathcal {F}}\\\\) whose vertex-sets partition \\\\(V(K_n)\\\\). This makes progress on a conjecture of Grinshpun and Sárközy.\",\"PeriodicalId\":50666,\"journal\":{\"name\":\"Combinatorica\",\"volume\":\"27 20\",\"pages\":\"\"},\"PeriodicalIF\":1.0000,\"publicationDate\":\"2023-11-21\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"2\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Combinatorica\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00493-023-00072-1\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Combinatorica","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00493-023-00072-1","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 2

摘要

我们证明，对于所有整数\(\Delta ,r \ge 2\)，存在一个常数\(C = C(\Delta ,r) >0\)，使得对于含有\(v(F_n) = n\)和\(\Delta (F_n) \le \Delta \)的图的每一个序列\({\mathcal {F}}= \{F_1, F_2, \ldots \}\)，对于每一个\(n \in {\mathbb {N}}\)，都成立如下式。在每个r边颜色的\(K_n\)中，有一个来自\({\mathcal {F}}\)的最多C个单色副本的集合，其顶点集分区为\(V(K_n)\)。这在Grinshpun和Sárközy的猜想上取得了进展。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

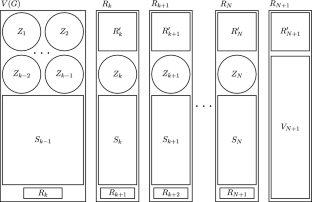
Tiling Edge-Coloured Graphs with Few Monochromatic Bounded-Degree Graphs

查看原文本刊更多论文

Tiling Edge-Coloured Graphs with Few Monochromatic Bounded-Degree Graphs

We prove that for all integers \(\Delta ,r \ge 2\), there is a constant \(C = C(\Delta ,r) >0\) such that the following is true for every sequence \({\mathcal {F}}= \{F_1, F_2, \ldots \}\) of graphs with \(v(F_n) = n\) and \(\Delta (F_n) \le \Delta \), for each \(n \in {\mathbb {N}}\). In every r-edge-coloured \(K_n\), there is a collection of at most C monochromatic copies from \({\mathcal {F}}\) whose vertex-sets partition \(V(K_n)\). This makes progress on a conjecture of Grinshpun and Sárközy.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Combinatorica 数学-数学

CiteScore

1.90

自引率

0.00%

发文量

审稿时长

>12 weeks

期刊介绍： COMBINATORICA publishes research papers in English in a variety of areas of combinatorics and the theory of computing, with particular emphasis on general techniques and unifying principles. Typical but not exclusive topics covered by COMBINATORICA are - Combinatorial structures (graphs, hypergraphs, matroids, designs, permutation groups). - Combinatorial optimization. - Combinatorial aspects of geometry and number theory. - Algorithms in combinatorics and related fields. - Computational complexity theory. - Randomization and explicit construction in combinatorics and algorithms.