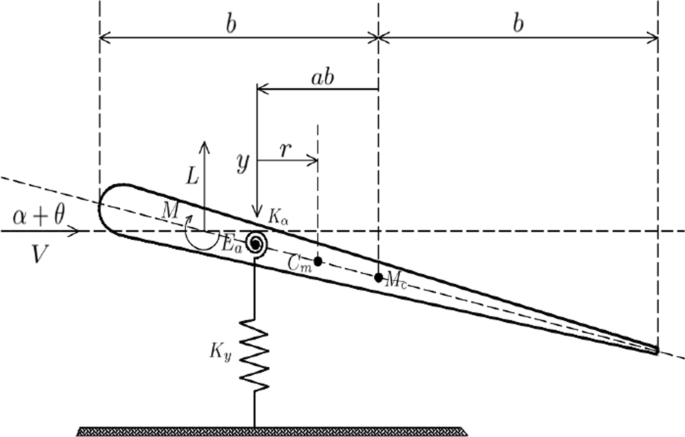
An Investigation of Dynamical Behavior of a Wing Model

Abstract Bifurcations of equilibria of a wing model have been investigated in this paper. It is shown that the quintic nonlinear terms in the pitch and the plunge coordinate have affected the bifurcation structure of nontrivial equilibria in different degree. In contrast with the quintic stiffening parameter in plunge, the quintic parameter in pitch has a relatively significant effect, which will affect the number, position and stability of nontrivial equilibria. Therein two pairs of nontrivial equilibria with opposite stability coexist or disappear by two fold bifurcations. If the freestream velocity has been taken as a continuation parameter, it will affect the bifurcation structure of all the equilibria, including the trivial and the nontrivial. Wherein the equilibria vary from a trivial to two nontrivial ones by a pitchfork bifurcation. Then one of nontrivial equilibria experiences a supercritical Hopf bifurcation and the bifurcated limit cycles form an ellipsoidal structure with the limit cycles bifurcated from the trivial equilibrium.