On Maximizing Sums of Non-monotone Submodular and Linear Functions

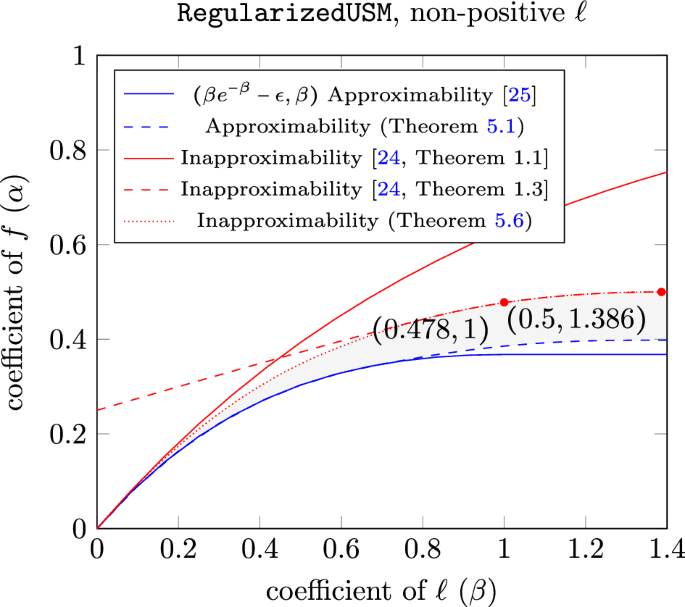
We study the problem of Regularized Unconstrained Submodular Maximization (RegularizedUSM) as defined by Bodek and Feldman (Maximizing sums of non-monotone submodular and linear functions: understanding the unconstrained case, arXiv:2204.03412, 2022): given query access to a non-negative submodular function \(f:2^{{\mathcal {N}}}\rightarrow {\mathbb {R}}_{\ge 0}\) and a linear function \(\ell :2^{{\mathcal {N}}}\rightarrow {\mathbb {R}}\) over the same ground set \({\mathcal {N}}\), output a set \(T\subseteq {\mathcal {N}}\) approximately maximizing the sum \(f(T)+\ell (T)\). An algorithm is said to provide an \((\alpha ,\beta )\)-approximation for RegularizedUSM if it outputs a set T such that \({\mathbb {E}}[f(T)+\ell (T)]\ge \max _{S\subseteq {\mathcal {N}}}[\alpha \cdot f(S)+\beta \cdot \ell (S)]\). We also consider the setting where S and T are constrained to be independent in a given matroid, which we refer to as Regularized Constrained Submodular Maximization (RegularizedCSM). The special case of RegularizedCSM with monotone f has been extensively studied (Sviridenko et al. in Math Oper Res 42(4):1197–1218, 2017; Feldman in Algorithmica 83(3):853–878, 2021; Harshaw et al., in: International conference on machine learning, PMLR, 2634–2643, 2019), whereas we are aware of only one prior work that studies RegularizedCSM with non-monotone f (Lu et al. in Optimization 1–27, 2023), and that work constrains \(\ell \) to be non-positive. In this work, we provide improved \((\alpha ,\beta )\)-approximation algorithms for both RegularizedUSM and RegularizedCSM with non-monotone f. Specifically, we are the first to provide nontrivial \((\alpha ,\beta )\)-approximations for RegularizedCSM where the sign of \(\ell \) is unconstrained, and the \(\alpha \) we obtain for RegularizedUSM improves over (Bodek and Feldman in Maximizing sums of non-monotone submodular and linear functions: understanding the unconstrained case, arXiv:2204.03412, 2022) for all \(\beta \in (0,1)\). We also prove new inapproximability results for RegularizedUSM and RegularizedCSM, as well as 0.478-inapproximability for maximizing a submodular function where S and T are subject to a cardinality constraint, improving a 0.491-inapproximability result due to Oveis Gharan and Vondrak (in: Proceedings of the twenty-second annual ACM-SIAM symposium on discrete algorithms, SIAM, pp 1098–1116, 2011).