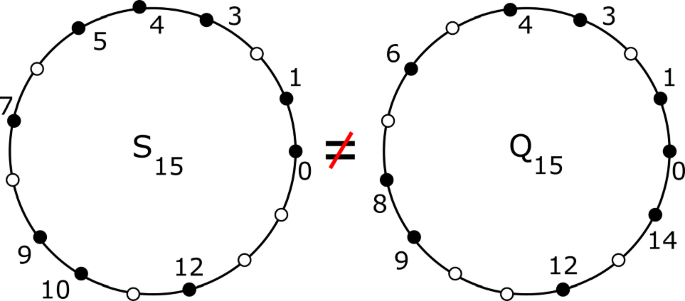
Density Functions of Periodic Sequences of Continuous Events

Abstract Periodic Geometry studies isometry invariants of periodic point sets that are also continuous under perturbations. The motivations come from periodic crystals whose structures are determined in a rigid form, but any minimal cells can discontinuously change due to small noise in measurements. For any integer $$k\ge 0$$ k ≥ 0 , the density function of a periodic set S was previously defined as the fractional volume of all k -fold intersections (within a minimal cell) of balls that have a variable radius t and centers at all points of S . This paper introduces the density functions for periodic sets of points with different initial radii motivated by atomic radii of chemical elements and by continuous events occupying disjoint intervals in time series. The contributions are explicit descriptions of the densities for periodic sequences of intervals. The new densities are strictly stronger and distinguish periodic sequences that have identical densities in the case of zero radii.