协方差聚类:当变量数量大于实验单元时,对设计实验中的协方差进行建模
IF 1.1
4区 数学
Q3 BIOLOGY
Journal of Agricultural Biological and Environmental Statistics
Pub Date : 2023-10-11
DOI:10.1007/s13253-023-00574-x
引用次数: 0
摘要
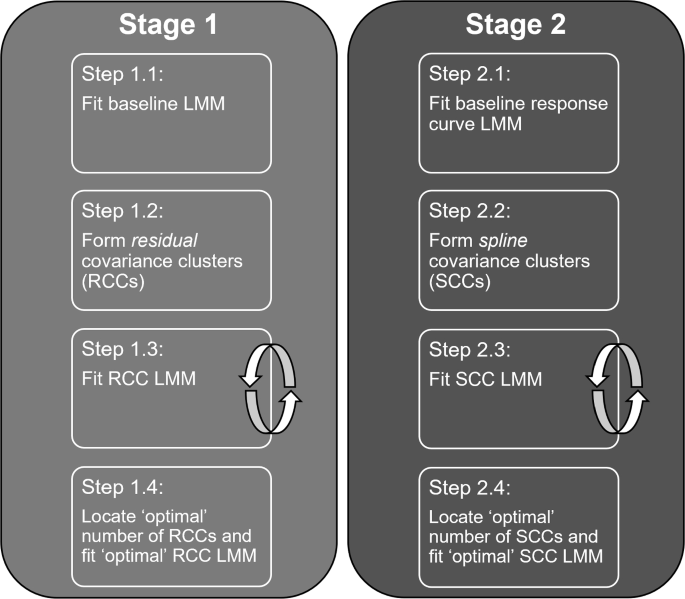
农业领域比较研究实验产生的数据集的规模和复杂性不断增加。在实验中测量的变量的数量经常超过组成实验的实验单元的数量。当需要对这些实验中存在的变量之间的协方差关系进行建模时,由于所得到的协方差结构的秩降低,可能会出现估计困难。本文提出了一种基于线性混合模型框架的统计方法,用于分析设计好的实验,其中数据集的特征是由比实验单元更多的变量组成,并且需要对变量之间的复杂协方差结构进行建模。在聚类算法的辅助下,该方法通过将协方差聚类作为随机效应引入建模框架来估计协方差,为构建协方差结构提供了传统方差分量模型的扩展。该方法应用于一项基于多相质谱的蛋白质组学实验,旨在探索大麦籽粒蛋白质组在酿造过程中随时间的变化。建模方法提供了一种新的基于线性混合模型的方法,用于估计设计实验中测量的变量之间的协方差结构,当有少量的实验单元或观测值时,通知协方差参数估计。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Covariance Clustering: Modelling Covariance in Designed Experiments When the Number of Variables is Greater than Experimental Units
Abstract The size and complexity of datasets resulting from comparative research experiments in the agricultural domain is constantly increasing. Often the number of variables measured in an experiment exceeds the number of experimental units composing the experiment. When there is a necessity to model the covariance relationships that exist between variables in these experiments, estimation difficulties can arise due to the resulting covariance structure being of reduced rank. A statistical method, based in a linear mixed model framework, is presented for the analysis of designed experiments where datasets are characterised by a greater number of variables than experimental units, and for which the modelling of complex covariance structures between variables is desired. Aided by a clustering algorithm, the method enables the estimation of covariance through the introduction of covariance clusters as random effects into the modelling framework, providing an extension of the traditional variance components model for building covariance structures. The method was applied to a multi-phase mass spectrometry-based proteomics experiment, with the aim of exploring changes in the proteome of barley grain over time during the malting process. The modelling approach provides a new linear mixed model-based method for the estimation of covariance structures between variables measured from designed experiments, when there are a small number of experimental units, or observations, informing covariance parameter estimates.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
2.70
自引率
7.10%
发文量
38
审稿时长
>12 weeks
期刊介绍:
The Journal of Agricultural, Biological and Environmental Statistics (JABES) publishes papers that introduce new statistical methods to solve practical problems in the agricultural sciences, the biological sciences (including biotechnology), and the environmental sciences (including those dealing with natural resources). Papers that apply existing methods in a novel context are also encouraged. Interdisciplinary papers and papers that illustrate the application of new and important statistical methods using real data are strongly encouraged. The journal does not normally publish papers that have a primary focus on human genetics, human health, or medical statistics.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


