拧开螺纹消除

IF 0.3 4区数学 Q1 Arts and Humanities

Archive for Mathematical Logic Pub Date : 2023-09-22 DOI:10.1007/s00153-023-00892-4

Gabriele Pulcini

{"title":"拧开螺纹消除","authors":"Gabriele Pulcini","doi":"10.1007/s00153-023-00892-4","DOIUrl":null,"url":null,"abstract":"<div><p>We provide a non-Gentzen, though fully syntactical, cut-elimination algorithm for classical propositional logic. The designed procedure is implemented on <span>\\(\\textsf{GS4}\\)</span>, the one-sided version of Kleene’s sequent system <span>\\(\\textsf{G4}\\)</span>. The algorithm here proposed proves to be more ‘dexterous’ than other, more traditional, Gentzen-style techniques as the size of proofs decreases at each step of reduction. As a corollary result, we show that analyticity always guarantees minimality of the size of <span>\\(\\textsf{GS4}\\)</span>-proofs.</p></div>","PeriodicalId":48853,"journal":{"name":"Archive for Mathematical Logic","volume":null,"pages":null},"PeriodicalIF":0.3000,"publicationDate":"2023-09-22","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://link.springer.com/content/pdf/10.1007/s00153-023-00892-4.pdf","citationCount":"0","resultStr":"{\"title\":\"Cut elimination by unthreading\",\"authors\":\"Gabriele Pulcini\",\"doi\":\"10.1007/s00153-023-00892-4\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>We provide a non-Gentzen, though fully syntactical, cut-elimination algorithm for classical propositional logic. The designed procedure is implemented on <span>\\\\(\\\\textsf{GS4}\\\\)</span>, the one-sided version of Kleene’s sequent system <span>\\\\(\\\\textsf{G4}\\\\)</span>. The algorithm here proposed proves to be more ‘dexterous’ than other, more traditional, Gentzen-style techniques as the size of proofs decreases at each step of reduction. As a corollary result, we show that analyticity always guarantees minimality of the size of <span>\\\\(\\\\textsf{GS4}\\\\)</span>-proofs.</p></div>\",\"PeriodicalId\":48853,\"journal\":{\"name\":\"Archive for Mathematical Logic\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.3000,\"publicationDate\":\"2023-09-22\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://link.springer.com/content/pdf/10.1007/s00153-023-00892-4.pdf\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Archive for Mathematical Logic\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00153-023-00892-4\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"Arts and Humanities\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Archive for Mathematical Logic","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s00153-023-00892-4","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"Arts and Humanities","Score":null,"Total":0}

引用次数: 0

摘要

我们为经典命题逻辑提供了一种非根岑（non-Gentzen）、但完全语法化的剪切消除算法。所设计的程序是在（textsf{GS4}\）上实现的，它是克莱因序列系统（sequent system \(\textsf{G4}\)）的单边版本。与其他更传统的根岑式技术相比，这里提出的算法被证明是更 "灵巧 "的，因为证明的大小在每一步缩减中都会减小。作为一个推论结果，我们证明了解析性总是保证了 \(\textsf{GS4}\) 证明的最小化。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

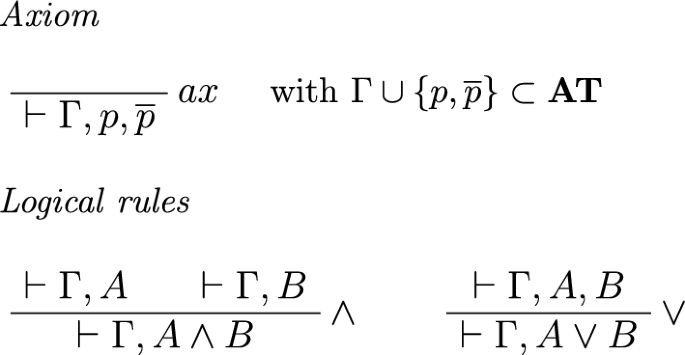
Cut elimination by unthreading

查看原文本刊更多论文

Cut elimination by unthreading

We provide a non-Gentzen, though fully syntactical, cut-elimination algorithm for classical propositional logic. The designed procedure is implemented on \(\textsf{GS4}\), the one-sided version of Kleene’s sequent system \(\textsf{G4}\). The algorithm here proposed proves to be more ‘dexterous’ than other, more traditional, Gentzen-style techniques as the size of proofs decreases at each step of reduction. As a corollary result, we show that analyticity always guarantees minimality of the size of \(\textsf{GS4}\)-proofs.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Archive for Mathematical Logic MATHEMATICS-LOGIC

CiteScore

0.80

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： The journal publishes research papers and occasionally surveys or expositions on mathematical logic. Contributions are also welcomed from other related areas, such as theoretical computer science or philosophy, as long as the methods of mathematical logic play a significant role. The journal therefore addresses logicians and mathematicians, computer scientists, and philosophers who are interested in the applications of mathematical logic in their own field, as well as its interactions with other areas of research.