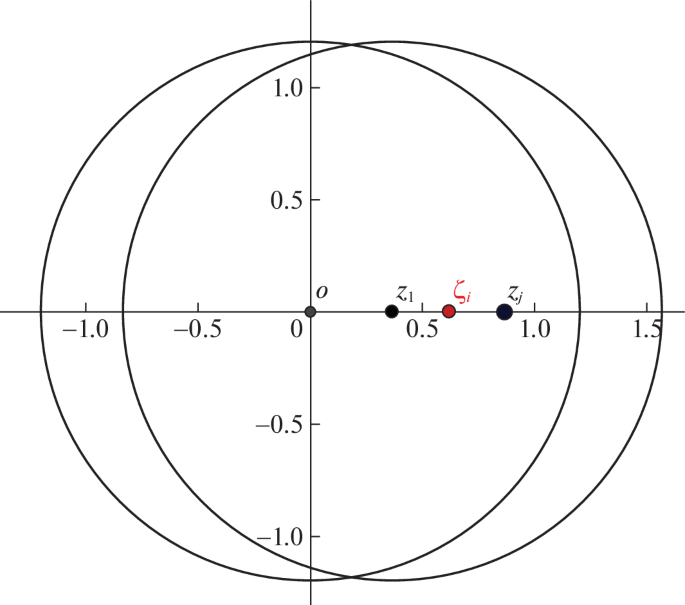
Distribution of Zeros and Critical Points of a Polynomial, and Sendov’s Conjecture

Abstract According to the Gauss–Lucas theorem, the critical points of a complex polynomial $$p(z):=\sum_{j=0}^{n}a_{j}z^{j}$$ where $$a_{j}\in\mathbb{C}$$ always lie in the convex hull of its zeros. In this paper, we prove certain relations between the distribution of zeros of a polynomial and its critical points. Using these relations, we prove the well-known Sendov’s conjecture for certain special cases.