一个动态高斯,对数正态,和反向对数正态卡尔曼滤波器
IF 3
3区 地球科学
Q2 METEOROLOGY & ATMOSPHERIC SCIENCES
引用次数: 1
摘要
我们推导了卡尔曼滤波器的一种泛化方法,该方法允许非高斯背景和观测误差。将高斯假设替换为考虑误差来自高斯、对数正态和反向对数正态随机变量的混合分布。我们详细介绍了反向对数正态误差的推导,并将结果扩展到混合分布,其中高斯、对数正态和反向对数正态状态变量的数量可以在每次分析时动态变化。我们基于Lorenz 1963模型在两个不同的系统上对动态混合卡尔曼滤波器进行了鲁棒性测试,并证明了与高斯卡尔曼滤波器相比,非高斯技术通常可以提高观测稀疏和不确定的分析技巧。这篇文章受版权保护。版权所有。本文章由计算机程序翻译,如有差异,请以英文原文为准。
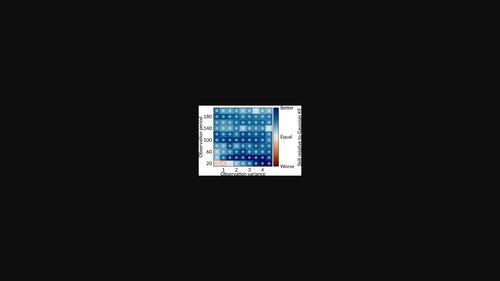
A dynamical Gaussian, lognormal, and reverse lognormal Kalman filter
Abstract We derive a generalization of the Kalman filter that allows for non‐Gaussian background and observation errors. The Gaussian assumption is replaced by considering that the errors come from a mixed distribution of Gaussian, lognormal, and reverse lognormal random variables. We detail the derivation for reverse lognormal errors, and extend the results to mixed distributions, where the number of Gaussian, lognormal, and reverse lognormal state variables can dynamically change every analysis time. We robustly test the dynamical mixed Kalman filter on two different systems based on the Lorenz 1963 model, and demonstrate that non‐Gaussian techniques generally improve the analysis skill if the observations are sparse and uncertain, compared to the Gaussian Kalman filter. This article is protected by copyright. All rights reserved.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
16.80
自引率
4.50%
发文量
163
审稿时长
3-8 weeks
期刊介绍:
The Quarterly Journal of the Royal Meteorological Society is a journal published by the Royal Meteorological Society. It aims to communicate and document new research in the atmospheric sciences and related fields. The journal is considered one of the leading publications in meteorology worldwide. It accepts articles, comprehensive review articles, and comments on published papers. It is published eight times a year, with additional special issues.
The Quarterly Journal has a wide readership of scientists in the atmospheric and related fields. It is indexed and abstracted in various databases, including Advanced Polymers Abstracts, Agricultural Engineering Abstracts, CAB Abstracts, CABDirect, COMPENDEX, CSA Civil Engineering Abstracts, Earthquake Engineering Abstracts, Engineered Materials Abstracts, Science Citation Index, SCOPUS, Web of Science, and more.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


