一维连续安德森哈密顿量的定位交叉
IF 3.6
1区 数学
Q1 MATHEMATICS
引用次数: 7
摘要
我们研究了具有白噪声势的连续安德森哈密顿函数$\mathcal{H}_{L}$的谱在一个长度$L$被发送到无穷长的段上的行为。我们放大1阶能级$E$(散装能级)或1阶能级$ L$(交叉能级)。我们证明了特征值和质心的点过程收敛于泊松点过程。我们还以显式的速率证明了本征函数的指数局域化。此外,我们证明了特征函数收敛于良好识别的极限:在交叉区域,这些极限是普遍的。结合我们的同伴论文(Dumaz and labb本文章由计算机程序翻译,如有差异,请以英文原文为准。
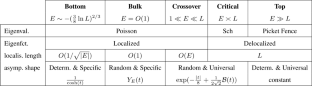
Localization crossover for the continuous Anderson Hamiltonian in 1-d
We investigate the behavior of the spectrum of the continuous Anderson Hamiltonian $\mathcal{H}_{L}$ , with white noise potential, on a segment whose size $L$ is sent to infinity. We zoom around energy levels $E$ either of order 1 (Bulk regime) or of order $1\ll E \ll L$ (Crossover regime). We show that the point process of (appropriately rescaled) eigenvalues and centers of mass converge to a Poisson point process. We also prove exponential localization of the eigenfunctions at an explicit rate. In addition, we show that the eigenfunctions converge to well-identified limits: in the Crossover regime, these limits are universal. Combined with the results of our companion paper (Dumaz and Labbé in Ann. Probab. 51(3):805–839, 2023), this identifies completely the transition between the localized and delocalized phases of the spectrum of $\mathcal{H}_{L}$ . The two main technical challenges are the proof of a two-points or Minami estimate, as well as an estimate on the convergence to equilibrium of a hypoelliptic diffusion, the proof of which relies on Malliavin calculus and the theory of hypocoercivity.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Inventiones mathematicae
数学-数学
CiteScore
5.60
自引率
3.20%
发文量
76
审稿时长
12 months
期刊介绍:
This journal is published at frequent intervals to bring out new contributions to mathematics. It is a policy of the journal to publish papers within four months of acceptance. Once a paper is accepted it goes immediately into production and no changes can be made by the author(s).
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


