基于调质分数Sturm-Liouville特征问题的高阶谱配置方法
IF 2.5
3区 数学
Q1 MATHEMATICS, APPLIED
引用次数: 0
摘要
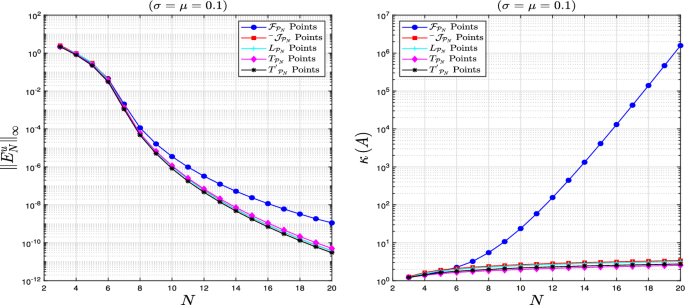
提出了一种精确的指数调质分数阶谱配置方法,用于求解一维时变调质分数阶偏微分方程(TFPDEs)。我们使用一组缓和分数Sturm-Liouville特征问题(TFSLP)作为基础,并使用分数拉格朗日插值(fli),这些插值通常在所使用的配点处满足Kronecker delta (KD)函数。首先,我们驱动相应的缓变分数微分矩阵(tfdm)。然后,我们处理了各种线性和非线性TFPDEs,其中包括空间回火分数阶平流扩散问题、时空回火分数阶平流扩散问题(TFADP)、多项时空回火分数阶问题和时空回火分数阶Burgers方程(TFBE),研究了分数阶配置方法的数值性能。研究包括对线性系统产生的条件数$$\kappa (A)$$ κ (a)的数值检验。从$$L^\infty $$ L∞范数误差和谱收敛指数速率的角度研究了该方法的精度和效率。本文章由计算机程序翻译,如有差异,请以英文原文为准。
High-order spectral collocation method using tempered fractional Sturm–Liouville eigenproblems
Abstract This paper presents an accurate exponential tempered fractional spectral collocation method (TFSCM) to solve one-dimensional and time-dependent tempered fractional partial differential equations (TFPDEs). We use a family of tempered fractional Sturm–Liouville eigenproblems (TFSLP) as a basis and the fractional Lagrange interpolants (FLIs) that generally satisfy the Kronecker delta (KD) function at the employed collocation points. Firstly, we drive the corresponding tempered fractional differentiation matrices (TFDMs). Then, we treat with various linear and nonlinear TFPDEs, among them, the space-tempered fractional advection and diffusion problem, the time-space tempered fractional advection–diffusion problem (TFADP), the multi-term time-space tempered fractional problems, and the time-space tempered fractional Burgers’ equation (TFBE) to investigate the numerical capability of the fractional collocation method. The study includes a numerical examination of the produced condition number $$\kappa (A)$$ κ ( A ) of the linear systems. The accuracy and efficiency of the proposed method are studied from the standpoint of the $$L^\infty $$ L ∞ -norm error and exponential rate of spectral convergence.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Computational & Applied Mathematics
Mathematics-Computational Mathematics
CiteScore
4.50
自引率
11.50%
发文量
352
审稿时长
>12 weeks
期刊介绍:
Computational & Applied Mathematics began to be published in 1981. This journal was conceived as the main scientific publication of SBMAC (Brazilian Society of Computational and Applied Mathematics).
The objective of the journal is the publication of original research in Applied and Computational Mathematics, with interfaces in Physics, Engineering, Chemistry, Biology, Operations Research, Statistics, Social Sciences and Economy. The journal has the usual quality standards of scientific international journals and we aim high level of contributions in terms of originality, depth and relevance.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


