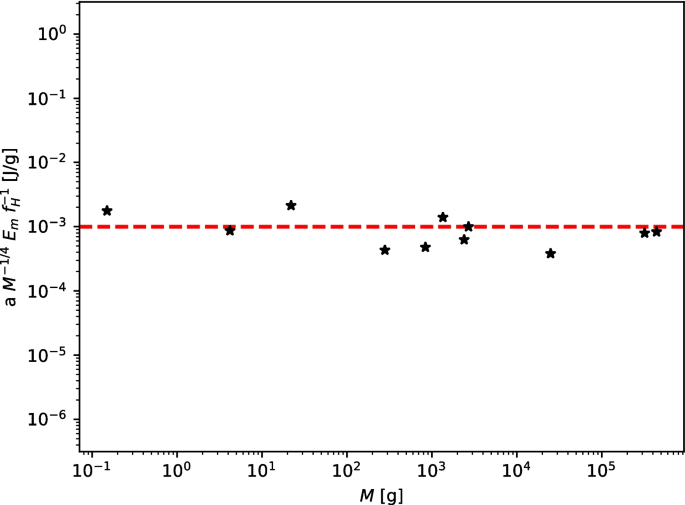
Universal ontogenetic growth without fitted parameters: implications for life history invariants and population growth

Abstract Since the work of von Bertalanffy (Q Rev Boil 32:217–231, 1957), several models have been proposed that relate the ontogenetic scaling of energy assimilation and metabolism to growth, which are able to describe ontogenetic growth trajectories for living organisms and collapse them onto a single universal curve (West et al. in Nature 413:628–631, 2001; Barnavar et al. in Nature 420:626, 2002). Nevertheless, all these ontogenetic growth models critically depend on fitting parameters and on the allometric scaling of the metabolic rate. Using a new metabolic rate relation (Escala in Theor Ecol 12(4):415–425, 2019) applied to a Bertalanffy-type ontogenetic growth equation, we find that ontogenetic growth can also be described by a universal growth curve for all studied species, but without the aid of any fitting parameters (i.e., no fitting procedure is performed on individual growth curves). We find that the inverse of the heart frequency $$\mathrm f_H$$ f H , rescaled by the ratio of the specific energies for biomass creation and metabolism, defines the characteristic timescale for ontogenetic growth. Moreover, our model also predicts a generation time and lifespan that explain the origin of several “Life History Invariants’ (Charnov in Oxford University Press, Oxford, 1993) and predict that the Malthusian parameter should be inversely proportional to both the generation time and lifespan, in agreement with the data in the literature (Duncan et al. in Ecology 88:324–333 2007; Dillingham et al. in Paper 535, 2016; Hatton et al. in PNAS 116(43):21616–21622 2019). In our formalism, several critical timescales and rates (lifespan, generation time, and intrinsic population growth rate) are all proportional to the heart frequency $$\mathrm f_H$$ f H , and thus, their allometric scaling relations come directly from the allometry of the heart frequency, which is typically $$\mathrm f_H \propto M^{-0.25}$$ f H ∝ M - 0.25 under basal conditions.