Separation Axioms in Soft Bitopological Ordered Spaces

This paper presents a comprehensive study on bi-ordered soft separation axioms applied to soft bitopological ordered spaces. The main focus of this research is to examine the properties, descriptions, and characteristics of these axioms. By exploring the relationships between these axioms and other properties of soft bitopological ordered spaces, this study expands our understanding of these spaces and their associated properties. Notably, significant findings are presented, establishing connections between the introduced bi-ordered axioms and properties such as soft bitopological and soft hereditary properties. The concepts of bi-ordered soft separation axioms, namely PSTi (resp. 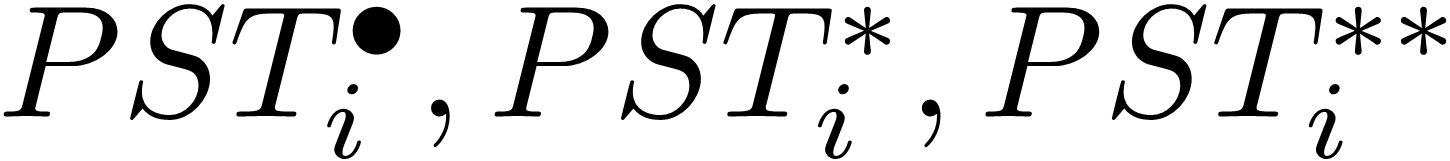)−ordered spaces, (where i = 0, 1, 2), are introduced and illustrated through relevant examples. These examples help clarify the relationships among the axioms and enhance our comprehension of their significance. Furthermore, this paper investigates the distinctions among separation axioms in topological ordered spaces and provides examples of relevant attributes from the literature. The separation axioms discussed in this research demonstrate enhanced descriptive power in characterizing the properties of topological ordered spaces. In addition to the above, the paper introduces the concept of bi-ordered subspace and explores the property of hereditary in the context of soft bitopological ordered spaces. These additions further enrich the understanding and applicability of bi-ordered soft separation axioms.